And miles to go before I sleep,
And miles to go before I sleep.
Robert Frost (1)
What is a mile? Nobody knows who invented the mile, which is now a part of the modern imperial system, used in the UK and the USA. It has been an official unit in England since at least 1593, when an order of Elizabeth I proclaimed:
"A Mile ſhall contain eight Furlongs, every Furlong forty Poles, and every Pole ſhall contain ſixteen Foot and an half."
There have been many kinds of mile in history, Roman miles, Greek miles, Irish and Scottish miles, nautical and country miles. It is often assumed that the mile is based on something vague, perhaps an imprecise measurement of the meridian. After all, in 1593 the scientific age was still in its infancy, the Copernican revolution only just begun.
The Roman mile or mille passus (thousand paces) was used as a unit of distance, and it is sometimes thought that a mile, the name referring to a thousand of something, is connected to the marching of an army. Sometimes it is believed that the mile comes from agriculture, being eight furlongs. The word "furlong" means a “furrow long”, i.e., the length of a furrow in an field, the distance that a team of oxen could plow in a session. Neither the ploughing of fields, nor the marching of soldiers is associated with high levels of precision. Sometimes it is believed the mile is just an arbitrary length, with no solid scientific foundation, no relation to anything in particular. Sometimes it is even believed that a high degree of precision was not really a thing humans were capable of, until the invention of the metre, and that we should not expect to find anything of significance in any unit of length prior to its invention. What if, on the contrary, the mile were an amazing cultural artefact from the distant past, proof that precision in measure existed well before 1791?
The number 864 and the sun
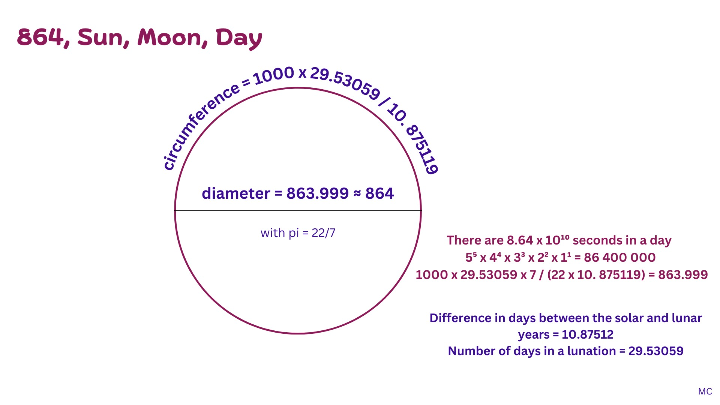
By coincidence, there are approximately 864 000 miles in the diameter of the sun, and 86 400 seconds in a day, i.e. a 24 hour period. 864 is an interesting number as it is 5⁵ x 4⁴ x 3³ x 2² x 1¹. Can we think of 864 000 as a solar number, and the mile as the way this number is expressed in the measure of the sun? An interesting aspect of the number 864 is that it can represent an aspect of the relationship between the orbits of the moon and the earth. With a lunation of 29.53059 days, the difference in days between the lunar and solar years as 10.875119 days, and with pi as 22/7, the number 864 000 can be approximated as: 1 000 000 x 29.53059 x 7/22 x 1/10.875119 = 863 999.448. So the size of the sun, the length of a day, and the orbits of the sun and the moon, are all linked through the number 864, the mile, the second, and the day. These coincidences beg the question of how the second and the mile were designed. Were the length of time it takes for the earth to turn on its axis, and the diameter of the sun deliberately divided into units that would result in the number 864?
The ancient traditions of the Indians, Chaldeans, and others, may give us a clue as to the mile's age, if we understand the mile to be part of a system in which certain numbers were preferred, and which was incredibly accurate in its ability to predict astronomical events, and in time-keeping. There are many ways in which we might divide a day. We use 24 hours, each made up of 60 minutes, each minute being made up of 60 seconds. In the incredibly precise Hebrew calendar, as well as seconds, there are also parts or chalakim of 3¹/³ seconds, and each hour is divided into 1080 of these parts, amounting to 25920 parts per day. These numbers, 25920, 1080, and 864 are all multiples of 54, 27 and 9, and are also found in the ancient Indian tradition, in which there are four cyclic ages on earth. The Satya Yuga is 1.728 million years, the Treta Yuga is 1.296 million years, the Dwapara Yuga is 0.864 million years, and the Kali Yuga is 0.432 million years. Within this system, 0.864 million years are 2,400 divine years, and the cycle gives a total of 4.32 million human years, which is half of 8.64 million. An age of Brahma is 100 years. Each year of Brahma has 360 days and 360 nights. The total age of Brahma is 360 x 100 x 8.64 billion = 311,040 billion human years. i.e. 311.04 trillion years, and this period is called "maha kalpa". If 360 is associated with the geometry of the circle, 864 is linked to the passing of time, as measured in years, and this of course is connected to the sun.
Where might this connection come from? 864 is exactly one thirtieth part of the traditional figure given to the length of a precessional cycle, or Great Year, in years, 25,920 (6⁴ x 20). The solar and lunar years, and the wobble of the earth’s spin on its own axis which causes precession, are all connected to the number 864. The Àryabhatiya of Àryabhata states:
In a yuga the revolutions of the Sun are 4,320,000, of the Moon 57,753,336, of the Earth eastward 1,582,237,500, of Saturn 146,564, of Jupiter 364,224, of Mars 2,296,824 . . . (10)
According to a French 18th century text by the astronomer Le Gentil, ancient Indian astronomers relied on the number 54 as the basis of many of their astronomical calculations because, at a time when their astronomy was at its peak, the rate of precession was calculated as 54 seconds per year. It seems these ancient astronomers observed that the stars advanced annually by 54 seconds from West to East. The number 54 is 864 / 16. “By means of this movement of 54 seconds, they formed periods of several million years; they introduced them into their religion, as indicating the age of the world, what it must still last.“ The rate at which the stars advance over a year as viewed from earth depends on the rate of precession as well as the obliquity of the earth's tilt. It's not clear whether the ancient astronomers of India equated precession with the observed motion of the stars over years. While this figure of 54 seconds does not work today, it may have been correct many centuries ago. Indeed, Le Gentil writes in his memoir that he was astounded by the accuracy and complexity of the ancient astronomical tables he found, which was in stark contrast with the practical astronomical abilities he found there during his stay.
It does not seem easy to me to know from where the Brahmins have drawn this precession from the Equinoxes of 54 seconds per year, all the more so because they do not know practical Astronomy. If they observe the eclipses of the Sun and the Moon, it is solely for a reason of religion; but if we suppose that this precession of the Equinoxes of 54 seconds comes from the Brahmins, and that they recognized this movement by a long flight of observations, the annual movement of the Stars would be slower today than it would not have been then, since it is only found 50 seconds. (2)
The ancient astronomers may have compensated for any discrepancies in their observations by refining their mathematical models to achieve accurate predictions. While the rate of precession might have been slightly different in ancient times, the figure of 54 seconds per year could have been a practical and accurate representation of their observations at a particular time. It was associated with periods representing millions of years. The number 54, and its double 108, have cultural and religious significance in the ancient Indian tradition. They are also important in geometry, as the angles of a pentagon reflect these values.
The use of these numbers, 54, 108, 864 and 25920, being all connected by simple multiples, must all date back to a time, way back in the past, when precession was estimated annually as 54 seconds from west to east. As Le Gentil observes, the Chaldeans had two astronomical periods, the neros of 50 years, and the saros of 3600 years, both of which are contained exactly within a 24 000 year period, which relates simply to an annual movement of the stars of 54 seconds, as in a 24 000 year period, assuming the rate to be constant, 54 seconds per year amount to a total of 1 296 000 seconds (6⁴ x 1000), or 360 hours, or 15 days. We might surmise, as Le Gentil does, that the two systems are connected, and rely on a measure of 54 seconds per year, and the number 6. We can also link these two traditions to the Hebrew calendar, which uses the numbers 108 and 25920, and to the Middle Eastern traditions that preceded it.
The number 12 is associated with a year of course, we have 12 months in a year, and between 12 and 13 lunar months in that period. There are 12 constellations (officially) that the sun travels through over the course of a year. And we divide up a day, as a rotation of the earth on its axis, as 12 x 2 hours. In the40,075.017 km (24,901.461 mi), an ancient text on astronomy and time keeping from the Vedic period, Jupiter's cycle is shown to be 60 years, and there is also a second cycle of almost 12 years, corresponding to a single sidereal revolution of the planet (it is in fact estimated as 11.862 years now) (5). The number 360 also corresponds to an astronomical count. The Sûrya Siddhânt also shows that a solar day is the "time during which the sun traverses each successive degree of the ecliptic, with his true motion, and its length accordingly varies with the rapidity of his motion: three hundred and sixty such days compose the sidereal year." (6) The numbers 6 and 12 are important in the imperial system of measure, as there are 12 inches in a foot, and 6 feet in 2 yards.
The ancient Indian texts, especially from the Vedic period, show with what precision astronomers worked at that time. In the Sûrya Siddhânta, a year is estimated as 365.2421756 days, which is only 1.4 seconds shorter than the modern value of 365.24219 days, and the sidereal year, the actual length of the Earth’s revolution around the Sun, as 365.2563627 days, which is virtually the same as the modern value of 365.25636305 days. There are also very good estimates for the diameters of the planets Mercury, equivalent to 3 008 miles, (currently accepted diameter 3,032 miles) and Saturn, equivalent to 73,882 miles (currently accepted diameter 74,580 miles). It is thereforec plausible that astronomers from this time were able to correctly determine the size of the sun, and of the moon.
The moon and the earth
The moon’s equatorial diameter is 2160 miles, which is 2 x 1080 miles, or 40 x 54, or 6³ x 10, and a multiple of 9. Again, we might ask ourselves how it was the mile was designed so as to fit precisely 2160 times into the moon’s equatorial diameter, and 864 000 times (not quite as precisely) into the sun’s diameter. There is a natural coincidence at play here of course, the sun being almost exactly 40 times bigger than the moon. But there is also clearly a system at work. 1080 is important in the Hebrew calendar, and according to Irv Bromberg, an expert on the Hebrew calendar, there are 1080 parts or chalakim in an hour, and "the Vilna Gaon similarly explained that only the division of hours into 1080 parts allows the duration of the lunation to be expressed without use of a fraction." (see Bromberg, Irv, Why Divide Hours into 1080 Parts? (utoronto.ca)) What about the size of the earth?
The equatorial circumference of the earth is 24,901.461 miles, and this can be understood as 365.242199 x 360,000 =131,487,191.64 feet, which make 24,902.877 miles. This is particularly interesting, as each rotation of the earth around its axis produces a day, which it seems can be measured in feet as a product of the number of degrees in a circle, and the number of days in a year, multiplied by 1000.
The number 4320 holds significance in ancient Indian cosmology and is often associated with the concept of Yugas, which represent different ages or epochs in the cyclical nature of time. The Yugas are part of the larger time scale in Hindu cosmology known as the "Maha Yuga" or "Chatur Yuga," which consists of four smaller Yugas. The Satya Yuga (Golden Age) is 1,728,000 years, the Treta Yuga (Silver Age) is 1,296,000 years, Dvapara Yuga (Bronze Age) is 864,000 years, and the Kali Yuga (Iron Age) is 432,000 years, and our present age. The sum of the durations of these four Yugas makes one Maha Yuga, and it totals 4,320,000 years.
Additionally, there is a concept of a larger cosmic cycle known as the "Kalpa" or "Day of Brahma," which includes 1,000 Maha Yugas. The duration of one Kalpa is, therefore, 4,320,000,000 years.
The recurrence of the number 4320 in various temporal cycles reflects the cyclical and systematic understanding of time in Hindu cosmology. A year of 365.242199 days multiplied by 4 320 000 gives the equatorial circumference of the earth in inches. The precision of this measure for the earth is astounding, as modern day estimates for the equatorial circumference are 40,075.017 km, or 24,901.461 miles. And the value in inches obtained by 365.242199 x 4 320 000 is 1 577 846 299.68, which is 24 902.8772045 miles, or 40 077.296 km, less than a mile and a half difference. (Or, to use the value for a year in days used in the Sûrya Siddhânt of 365.2421756, the circumference is 24 902.8756 miles, or 40 077.293444 km). This simple coincidence tells us that the day inch must have existed in ancient India, as this calculation shows the connection in inches and days between the turning of the earth on its axis around the sun. And secondly that the scientific abilities of the people who were contemporary with the design of these ancient systems, in which the yugas are set out, is absolutely incredible.
Interestingly, the connection between the circumference of the earth and the number 4320 is also to be found in Egypt, which offers proof of the connection between these two ancient cultures, India and Egypt. Graham Hancock discusses this in his Fingerprints of the Gods, (8) first published in 1995, showing that the perimeter of the Great Pyramid was equal to the circumference of the earth divided by 43 200, and the polar radius corresponded to the height of the Great Pyramid in the same manner. Randall Carson has refined this by distinguishing between an inner and outer perimeter of the Great Pyramid, the inner corresponding to the polar circumference, and the outer corresponding to the equatorial. (9)
The polar circumference is 24,859.734 miles, and this can be approximated as 1 575 000 000 inches. The average of these two circumferences is 24,880.5975 miles, which is very close to 12⁵/10 = 24,883.2 miles. While multiples of 6 or 9 expressed in miles don't seem to fit quite as precisely with the equatorial and polar circumferences of the earth, the inch and the foot do, and the average circumference is very close to 12⁵/10 miles. With the equatorial circumference of the earth, especially, it’s as if the foot were a division of the constant spinning of the earth around its axis. If we were to take a particular point on the equator, and follow it as the earth spins over a year, over several years, not counting the actual length of the orbit of the earth round the sun, the point travels 1000 feet times 360 degrees, on average 365.242199 times per year. So it makes good sense to define the foot in terms of this motion. The earth's equatorial diameter is 7,926.3812 miles, and the polar diameter is 7,913.0991 miles. These figures, not being multiples of 9 or 6, not even being integers, don't suggest that the mile is also a subdivision of the diameter, as part of a particular system of numbers, as with the sun and moon. Perhaps, however, we could think of the equatorial diameter as √(10,000,000 π) x √2?
One mile is approximately equal to earth’s equatorial circumference divided by √(π3 x 20,000,000) = √(10,000,000 π) x √2 x π /earth’s equatorial circumference. According to Hugh Franklin, the number 24,902.31984, which is very close to the contemporary figure for the equatorial circumference of the earth in miles, is in fact √(π3 x 20,000,000). So if you have a circle with a circumference of 24,902.31984 miles, and the diameter of this circle can also be the diagonal of a square. The square will have a side of 24,902.31984 /(√2x π) miles, and the area of this square will be 10,000,000 π square miles. This square would be equal in area to a circle with a diameter of 10,000,000 miles. This would suggest that the equatorial circumference of our planet, via the geometries of the circle and the square, gave rise to the mile itself, as a unit of measure. The circumference of the earth as a value in miles is equated to a square with an area of 10,000,000 π. So we can define a mile as the earth’s equatorial circumference divided by √(π3 x 20,000,000). Or alternatively a mile can be described as √(10,000,000 π) x √2 x π divided by the earth’s equatorial circumference. This is of course purely conjecture. There is however solid evidence that the mile existed in ancient India, and that it fits with key Sumerian units.
Indian units of measure
We've seen that the mile fits in well with the moon, the sun and the number system which includes 54, 108, 2160 and 25920. The mile is linked very precisely to ancient Indian units of length. In traditional Indian measures, a Yojana is 14.484096 Km, which works out at exactly 9 miles. According to Chanakya, in the 4th century BC, there are two types of a unit called the Dhanusha, used for measuring lengths and distances. The ordinary Dhanusha is 96 Angulas, and the other Dhanusha, “Garhpatya Dhanusha”, is 108 Angulas, used for measurement of roads and distances. According to Chanakya, a Dhanurgraha consists of 4 Angulas and a Yojana consists of 8000 Dhanushas. In 1930-31, at Mohenjo-daro, Ernest Mackay discovered a broken piece of shell bearing 8 divisions of 6.7056mm each, which is equivalent to 0.264 inches, which multiplied by 8 is 2.2 inches. With pi as 25/8, in keeping with the 8 divisions, a diameter of 8 divisions of 6.7056 mm, or 0.264 inches, which is 4 Angulas, gives a circumference of 10 divisions of 16.764 mm, or 0.66 inches, which is 10 angulas. 96 Angulas make an ordinary Dhanusha, and this is exactly a thousandth part of an English mile. A Yojana of 8000 Dhanusha (of 108 Angulas each) is 9 miles and 1000 Dhanushas of 96 Angulas each are 1 mile. The word mile means thousand in Latin, and so it is curious that a thousandth part of a mile is this Indian unit of measure called a Dhanusha. The sushi of ancient Sumeria, preserved on a statue of Gudea, in the Louvre, is 0.66 inches long, and so is equal to 2 angulas. This particular system of measure, to which the mile is attached, goes back far in time, is rooted in astronomy, and a number system that is centered on the numbers 9, 54, 108 and 25920, and has wide geographical roots.
Musings on the mile
It is possible that the mile was designed in Vedic times, in ancient India, or even before that, as a result of computations regarding the sizes of the earth, the moon and the sun, a common unit to describe them all within a certain framework of numbers. The geometry of the circle is central to the relationship between many ancient units of measure. Pi itself can be approximated as 1 lunation / difference in days between twelve lunar months and a year divided by 0.864. Could we think of the mile as somehow connected to both time and space, and the circle?
A mile is 5280 feet, and the number 5280 can be approximated by a movement of the moon, together with the difference in days between a solar and lunar year. 70,000 lunations of 29.53059 days, divided by 36, and then divided again by 10.875119, the difference in days between solar and lunar years, is 5279.9966. So one mile, in feet, can be defined as 70,000 lunations / (36 x the difference in days between solar and lunar years). Since the equatorial circumference of the earth is 365.242199 x 360,000 =131,487,191.64 feet, or 24,902.877 miles, it can also be described as 70,000 lunations x (√(π3 x 20,000,000) / ( 36 x the difference in days between solar and lunar years) feet. This can be simplified to √(10,000,000 π) x √2 x π x 5,280 feet. Consequently, the equatorial circumference of the earth in miles is 365.242199 x 1,296 x the difference in days between solar and lunar years / 7 lunations, and the meridian circumference of the earth is 1752 x 10,000,000 lunations / ( 3 x the difference in days between solar and lunar years x 176) inches. The earth’s equatorial circumference in feet is 70,000 lunations x (√(π3 x 20,000,000) / ( 36 x the difference in days between solar and lunar years), which simplifies to √(10,000,000 π) x √2 x π x 5,280 feet. And the equatorial circumference of the earth in miles is 365.242199 x 1,296 x the difference in days between solar and lunar years / 7 lunations. The meridian circumference of the earth becomes 175²
x 10,000,000 lunations / ( 3 x the difference in days between solar and lunar years x 176) inches. While the word "mile" implies a thousand units, and we have seen that it is a thousand Dhanusha, it is perhaps also useful to think of it as 5280 feet.
The relation between the solar and lunar years can be expressed as pi multiplied by the length of a precessional cycle or Great Year (traditional value) divided by 30,000. If one thousand lunar months of 29.53059 days and the number of days difference between the solar and lunar years, 10.875119, then divided by pi as 22/7, gives 864, then 3,000 lunar months give, in the same way, the precessional cycle: 30,000 x 29.53059/10.875119 x (7/22) = 25,919.983, almost 25,920.
It does not come as a surprise that the mile should be part of a sophisticated system of measure when we look at other ancient, and modern units, and the work that has been done on them by independent researchers, proving that the size of the earth was known at some time to the ancients. For example, we can think of the polar circumference of the earth as 1 575 000 000 inches, and 600,000 x 60 x 60 Roman or Egyptian digits of 0.729166667 inches. Jim Alison writes:
Given .5238 meters, or 20.62 inches, for the length of the royal cubit, the length of the remen is .3704 meters or 14.58 inches. The meridian circumference of the earth is 40,008,000 meters or 111,133 meters per average degree of latitude. 300,000 remen times .3704 equals 111,120 meters. 5000 remen equals one minute of latitude and 500 remen equals one tenth of one minute of latitude. Given 20.62 inches for the length of the royal cubit, the remen expresses the length of an average degree of latitude with greater accuracy than the modern meter, that was fixed before the exact length of the meridian circumference was known to its creators, and unlike the meter, the remen is in unity with minutes and degrees of latitude. Archaeological and textual evidence from throughout ancient Egyptian history, as well as textual evidence from ancient Greek and Roman sources, support a conclusion that the correspondence between the length of the remen and the royal cubit, and the meridian length of Egypt and the earth, was known to their creators.(4)
In addition, if we look at the dimensions of many ancient sites, from Stonehenge, to stone circles in the UK, Ireland and France, to the pyramids of Giza, they can produce intriguing results when read in inches and feet.
Conclusion
It is well known, from the work of Hero of Alexandria for example, that ancient units of measurement were derived from the size of the earth. Yet it is almost always assumed that the earth was only measured accurately very recently, and that ancient attempts were most probably way off the mark. A close examination of many ancient units shows that on the contrary they fit remarkably well with the planet's dimensions. Moreover, many units that have survived to this day within the imperial system, such as the mile, also reflect a precise measure of the earth, which goes back to long before recorded history. The mile also fits with the dimensions of the sun and the moon, as part of a number system in which numbers such as 864, 54, 9 and 6 are central pillars, and within the ancient Indian system of measure.
There is a possible link between the mile and the cycles of the sun and the moon. One lunation in days, 29.53059, divided by the average difference in days between the lunar year and the solar year, 10.87512 days, multiplied by 7,000/36, is 5,279.996. There are of course 5,280 feet in a mile, so if you take this to be a value in feet, it’s very close to a mile.
5,280 x 10.87512 x 36 / 70,000 = 29.5306
It seems that units of time (days) have been combined with the size of the earth and used to produce units of space (feet). If the foot itself is a product of temporal and spatial measurements - the girth of the Earth and it's path round the sun - perhaps something could be said of an understanding of the interdependence of space and time on behalf of its creators. Robin Heath describes the foot as ‘an astonishing enduring artefact bequeathed to us from the prehistoric world' (3), and this can perhaps also be said of the mile.
Because for so long Christian authorities came down so hard on anyone they didn't like, such as scientists, Pagans, heretics, women, Jews, Muslims, homosexuals, and many others, and because they had the power to injure and kill, and burn libraries all over the world, from Egypt to South America, we tend to associate the pre-Copernican Revolution period with the absence of proper science and mathematics. To understand the complexity of the tradition the systems of measure that produced the mile come from, we should remember that there have in fact been many periods in history when science flourished, in various parts of the world. In Europe in particular, the lack of economic and social stability in Europe following the collapse of the Roman Empire, which, combined with climate chaos, and outbreaks of plague and war, also greatly hindered scientific research. There have clearly been other times and places in which science flourished, and in particular, this is true of India, in the Vedic period, and of the ancient Middle East.
In England, if we measure the distance, centre to centre, between two of the most important ancient sites, Old Sarum and Stonehenge, it is exactly 6 miles. While it is unusual for an integer number of miles to be contained exactly between two megalithic sites, this suggests that the mile could have been used in the neolithic. In his book Stonehenge, Cracking the Megalithic Code, David Kenworthy writes:
The origin of the foot and the imperial system has always been a problem and the best fit found was that they [the megalith builders] understood how to measure the circumference of the earth, and the foot was the unit that harmonised the split of the circumference using 360 and 366 degree circles. (7)
We can perhaps try to understand the mile as part of an ancient, widespread system that was sophisticated and precise. Since Vedic times, while the length of a lunation has gradually decreased slightly, and the length of a solar year has increased slightly, the changes have beenre very small. The number of days in a lunar month divided by the difference in days between twelve lunar months and a year is very close to Pi as 22/7 times 0.864. Twelve lunar months of 29.53059 days give a lunar year of 354.36708 days. That’s 10.875119 days fewer than a solar year of 365.242199 days. Pi can be approximated as 1 lunation / difference in days between twelve lunar months and a year divided by 0.864.
Approximately, with 10.875119 as the difference in days between the solar and lunar years, and the 29.5306 as the number of days in a lunation, or lunar month:
one mile = earth’s equatorial circumference /( √(π3 x 20,000,000)
= √(10,000,000 π) x √2 x π /earth’s equatorial circumference
and the equatorial circumference of the earth
= 365.242199 x 360,000 =131,487,191.64 feet, or 24,902.877 miles
Consequently, earth’s equatorial circumference in feet
= 70,000 lunations x (√(π3 x 20,000,000) / ( 36 x the difference in days between solar and lunar years)
which is also, in miles, √(10,000,000 π) x √2 x π miles, or 365.242199 x 1,296 x the difference in days between solar and lunar years / 7 lunations
and the meridian circumference of the earth in miles is
= 175² x 10,000,000 lunations / ( 190 080 x the difference in days between solar and lunar years x 176)
Notes
1. Robert Frost, “Stopping by Woods on a Snowy Evening” from The Poetry of Robert Frost, edited by Edward Connery Lathem. Copyright 1923, © 1969 by Henry Holt and Company, Inc., renewed 1951, by Robert Frost. Reprinted with the permission of Henry Holt and Company, LLC. Collected Poems, Prose, & Plays (Library of America, 1995)
2. Le Gentil, Voyage dans les Mers de l'Inde, Tome 1 https://ia600308.us.archive.org/27/items/gri_33125012932865/gri_33125012932865.pdf 3 . Robin Heath and John Michell, 2006, The Lost Science of Measuring the Earth, p 43
4 ” The measure of the remen and the royal cubit and the meridian of Egypt and the Earth”, by Jim Alison, 2020, http://home.hiwaay.net/~jalison/blu5.PDF
5. Sûrya Siddhânta p 111
6. Sûrya Siddhânta p 111
7. Kenworthy, David, Stonehenge, Cracking the Megalithic Code, p 80
8. Hancock, Graham, Fingerprints of the Gods, 2019 edition p 418 Fingerprints Of The Gods By Graham Hancock : motivator8 : Free Download, Borrow, and Streaming : Internet Archive
9. Randall Carson lecture, see https://www.youtube.com/watch?v=R7oyZGW99os
10. The Àryabhatiya of Àryabhata, An Ancient Indian Work on Mathematics and Astronomy, translated by W. Clark, 1930)