A twenty metre square is a good place to start, to think about the Egyptian royal cubit. A side of 20 metres of 39.375 inches, a little over the length of the modern metre, can be multiplied by an approximation of Phi squared, 144/55, to produce 100 Egyptian royal cubits of 20.618181818 inches, or 0.52363636 metres. Another approximation of Phi squared produces a slightly different value for the Egyptian royal cubit: 20 metres x 55/21 gives 100 cubits of 0.5238095 metres, or 20 x 39.375 inches x 55/21 gives 100 cubits of 20.625 inches.

If we divide a side of this square by an approximation of Phi squared instead, we obtain the product of a cubit and a remen of 14.58333333 inches. With 21/55, we get 20 x 39.375 x 21/55 = 20.618181818 x 14.5833333. and with 55/144, we get 20 x 39.375 x 55/144 = 20.625.

The diagonal of this square can be estimated as 20 x 39.375 x √2 = 1113.6931804 inches, or 20 x 39.375 x 99/70, using an approximation for √2, gives 1113.75 inches, or in metres, this is 28.2842712 or 28.28571429 respectively. The diagonal of the reduced 20 x 21/55 metre square is 10.8 metres, or 425.25 inches, with 99/70 for √2. This diagonal is the product of the two Egyptian cubits we have just seen: 0.5238095 metres and 0.52363636 metres, which is 20.625 inches and 20.6181818 inches respectively, as David Kenworthy has shown. The diagonal of the reduced 20 x 55/144 square, also with 99/70, is 425.390625 inches, which is 20.625². Stephen Dail has connected 425.25 to both the lunation, as 29.53125 x 14.4 = 425.25, and to the draconic month, modified slightly to fit within the number system,

27.34375 x 15.552 = 425.25.

A double square can generate the Egyptian royal cubit. The 1:2:√5 triangle has a perimeter of Phi squared.

A square with sides of 20 centimetres can be extended into a golden rectangle, with sides of 20 cm and 20 x 144/55 cm. The diagonal would be √(3.14195 x 1000) cm, close to √(pix1000). Or with 55/21, the diagonal would be √(3.14376417 x 1000) cm.

The two values for the Egyptian royal cubit seen so far rely on two different approximations of Phi squared as factors, combines with a unit of 20 cm (which, to convert into inches, works best with a 39.375 inch metre). These two cubits can also be arrived at via approximations of Phi squared and pi, still courtesy of the metre, as Schwaller de Lubicz showed. The smaller cubit of 0.52363636 metres, or 20.6181818 inches, is also equal to pi - Phi² metres, using 864/275, an approximation or pi, and 144/55. 3.1418181818 - 2.618181818 = 0.5236363636 metres.

The larger cubit of 0.5238095 metres, or 20.625 inches, is arrived at with 22/7 for pi, and 55/21 for Phi squared. 3.142857 - 2.6190476 = 0.5238095 metres. The difference between pi and Phi squared produces the Egyptian royal cubit in metres. The metre is central to ancient metrology.

We can draw a square of side 1, and a line of length Phi, as below:

By adding these two lines we obtain Phi². If the square measured 20 cm on a side, we would thus obtain the Egyptian royal cubit.

We can convert the length of the circumference of the circle into a straight line (in blue).

And see the difference between the line of length Phi² and the line of length pi.

In metres, we know that π-Phi² gives the royal Egyptian cubit.

We know that Phi² x 6/5 gives pi, if we use the approximations 144/55 and 864/275, or 55/21 and 22/7. In the same way, if we multiply the difference between pi and Phi squared by 5, we obtain Phi². 5 x (864/275 - 144/55) = 144/55, and 5 x (22/7 - 55/21) = 55/21. Compared to our square with side 1, we have a length Phi², and if the square had sides of 20 cm, we would still have the Egyptian royal cubit here.

If we divide 5(π-Phi²) by Phi², we then get 1, and that brings us back to our starting square.

Phi²-π metres = Egyptian royal cubit

Several researchers have shown the connection between a unit of 39.375 inches and the moon, including Jim Wakefield, Jim Alison, Howard Crowhurst, Richard Heath, Dennis Payne and Stephen Dail. An approximation for the lunar month in days, 29.53125 fits in perfectly with the other approximations seen so far.

29.53125 x 4/3 = 39.375 is a metre in inches, and 29.53125 x 2/90 = 0.65625 is a shusi in inches. 27 metres represent 36 lunar months. 108 metres represent 144 lunar months, and are equal to 425.25 x 10 inches, which is, as we've seen, is the product of two different Egyptian royal cubits. This unit of 425.25 inches, or 10.8 metres, can be multiplied by Phi squared, approximated as 55/21, which is 20 x 99/70 metres, the diagonal of our 20 square metre square, and then multiplied by 7, to produce an old English measure, the rod, of 198 inches. So this rod can be understood as 7 x 20 x 99/70 inches, and also 7 x 425.25 x 55/21 x1/39.375 inches. And 20 metres are equal to 425.25 x 55/21 x 70/99 inches. The rod can be subdivided into 15 parts to produce the Saxon foot of 13.2 inches. The side of our 20 metre square can be multiplied by 54 to produce 100 royal Egyptian cubits squared in inches, that is, 54 x 20 metres =100 x 20.6181818 x 20.625 inches. The number 54 is key to the canonical number system, and is the number of seconds per year which the ancient Brahmins estimated the stars to move across the sky, from west to east, in the precessional cycle. (1)

A rectangle made up of 4 squares has interesting solar and lunar properties, as Richard Heath and Robin Heath have documented, with their work at Le Manio in Brittany. Half this rectangle creates a 4 :1:√17 triangle. The width, as 9 metres, represents 12 lunar months, or a lunar year. The length is 36 metres, representing 48 lunar months. And the diagonal represents 4 solar years. The length of 36 metres in fact gives a diagonal of 36 x 39.375 / 4 x √17 = 1461.125556 inches, which four solar years. The Egyptian Sothic cycle 1461 civil years of 365 days, 1460 Julian years of 365.25 days.

4 lunar months as 29.53125 days make 118.125 days. 118.125 inches are 3 metres of 39.375 inches.

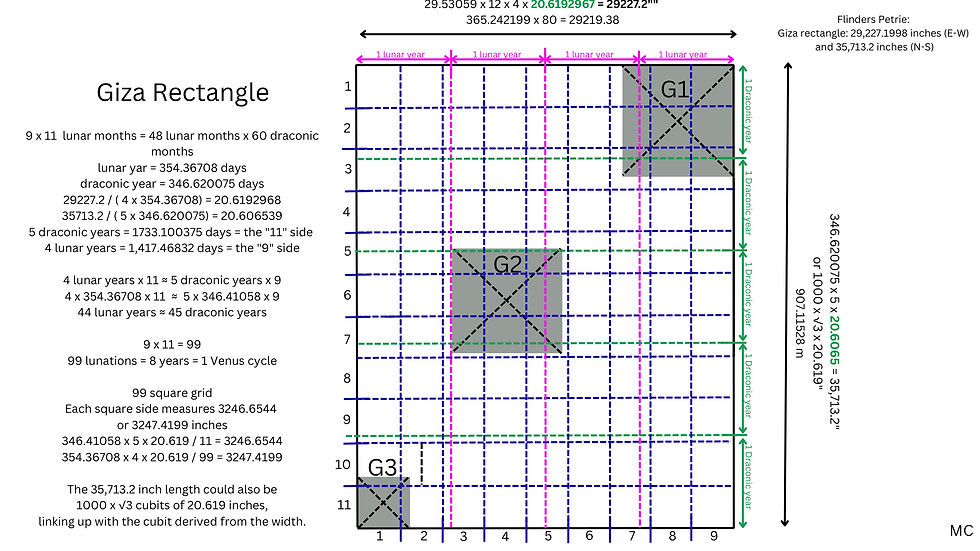
The width of the Giza rectangle, a rectangle made up by the outlines of the pyramids at Giza, also references 4 lunar years, but as part of a 9:11 rectangle.

A square of 20 metres is a useful shape when it comes to interpreting ancient measures. So it's interesting to find that the length of the station stone rectangle at Stonehenge, 80 x 33.3333 metres, within the Aubrey circle, is made up of 4 such squares side by side, and the width is 1 of these squares x 5/3. This point on the width is significant, in terms of Robin Heath's lunation triangle at Stonehenge.

The lunation triangle, discovered by Robin Heath, is a 5:12:13 Pythagorean triangle. (2) 12 and 13 are the number of possible lunations in a year, the average being 12.368266. Robin Heath has shown that several aspects of Stonehenge's design reflect a link between the year and the lunar cycle. A diagonal of 12.368266 would require a rectangle with a ratio between sides of 12 : 2.995. A rectangle with sides of 12 and 3 would have a diagonal which is very close to the average number of lunations in a solar year. These proportions can be found within the 5 :12 : 13 triangle, simply by dividing the 5 side at the 3 / 5 point. The hypotenuse will be 12.3693469, which is the square root of 153. The number 153 is itself a highly symbolic number, associated with 17, as it is 9 x 17, and related to the biblical story of the fish and the nets.(3) “Simon Peter went up and drew the net to land full of great fishes, one hundred and fifty and three.” (John 21.11). According to John Michell, "The key is the number 1224, which is the value by gematria of both το διχτυον, the net, and ιχθυες, fishes. 1224 is equal to 8 times 153, and 153 is the sum of numbers 1-17.” A 1x4 rectangle, with its √17 diagonal, is therefore significant with respect to lunar counting. When a 1x4 rectangle has sides of 9 and 36 metres, as at Le Manio, it's clear that the diagonal of 9√17 metres signifies 4 solar years in inches, as Richard Heath has demonstrated.(5) And if this 1x4 rectangle has side of 3 and 12 units, the diagonal will be 3√17 = 12.3693168, which represents the average number of lunations in a year, but does not depend on a particular unit of measure. If the sides of this 1x4 rectangle are 270 x 1080 inches, the diagonal will be 270√17 inches, which also works out very nearly as the diagonal of a 20 metre square, as 270 x √17 x 70/99 = 787.13835 inches.

The square root of 153 can be rounded to 12.369, and 369 is a number associated with the moon, in the lunar magic square, in which all rows, columns and diagonals have a sum of 369, and is composed of 9 smaller magic squares which also reference 369. Alexander Thom found that dividing lengths into 17 parts could be helpful, as with his work at Mid Clyth for example, where he tells us he divides 65 megalithic fathoms, i.e. 65 x 5.44 feet, into 17 parts, each 7.77 feet. (4)

A length of 17 Megalithic Yards would be significant within a lunar context, if associated with Jim Wakefield's 47 Saxon feet.

At Stonehenge, the length of these two superimposed triangles is the 12 side, and is 80 metres long. The '5' side of the larger Pythagorean triangle is 33.333 metres long, and the '3' side of the smaller triangle is 20 metres long. This means that the triangle found at Le Manio, having proportions of 1:4:√17, can be found at Stonehenge also, in that the lower half of the Pythagorean 5:12:13 triangle, created by removing the 3:12:12.3693169 triangle, is precisely the Le Manio triangle, on a different scale. Indeed, 3 x √17 = 12.3693169, is approximately the average number of lunar months in a year. This means that the length represents 106.66667 lunations, the 26.66667 lunations, the two sides combining to represent 400/3 lunations. Perhaps the 80 metres of the length of the rectangle reference Venus, and 8 x 3 x √17 = 98.95, close to 99, the number of lunations in 100 years. Many Fibonacci numbers appear in this geometry, so far we've come across 3, 5, 8, 13, 21, 55 and 144.

At Stonehenge, this geometry is underpinned by a spiral of Theodorus contained within the Aubrey circle. This kind of spiral is made up of consecutive right-angled triangles with hypotenuses of √2, √3, √4, etc, all the way to infinity, or to √17 before these triangles start overlapping on to each other. This particular one starts off with a square of 20 x 20 metres. the width of the Station Stone rectangle is 33.33333 metres, so this square represents two thirds of the width, a perfect fifth. 5/3 is also 2 Phi² / π, with 144/55 for Phi² and 144/55 x 6/5 for pi, or with 55/21 and 22/7.

This square also has sides that are a quarter of the length of this rectangle. This 20 x 20 metre square is then swiveled round so that one corner coincides with the corner of the Station Stone rectangle, and the base is aligned with this rectangle's diagonal. The hypotenuse of √16 on the second largest triangle matches the length of the Station Stone rectangle, and the hypotenuse of √17 matches the diagonal of the 1:4 rectangle, meeting the opposite side of the Station Stone rectangle at the 2:3 point.

If we take 80 metres and 33.3333 metres as the sides of the Station Stone rectangle, at Stonehenge, the diagonal is 86.66667 metres, and is the diameter of the Aubrey circle. The circumference is then 272.27136 metres, which is very close to 10 x 27.212 metres, 27.212 being the length in days of a draconic month. The circumference is then also 520 Egyptian royal cubits of 20.625 inches, if we use pi as 22/7, or 520 cubits of 20.6181818 inches with pi as 864/275, 52 being the number of weeks in a year. The area is close to 100 000 x 365.25 square inches. (If the metre were 39.342635 inches, this would be closer still.)

The Station Stone rectangle could possibly also be compatible with a Phi connection. The proportions are slightly different to a 5:12 rectangle.

A circle with a diameter of 20 x 144/55 metres would have a circumference of 6 480 inches, or 540 feet, with pi = 22/7.

A 20 metre square is at the root of the Egyptian royal cubit, and lunar megalithic geometry. But the inch is also part of the picture. A square with sides of 1000 x 21/55 x 21/55 x 55/144 inches has a diagonal of 2 metres of 39.375 inches. And the inch can also generate the Egyptian royal cubit through the square, if the square has a side of 100 x 21/55 x 21/55 inches, the diagonal will have a length of 20.6181818 inches, using 99/70 for the square root of 2.

The simple geometry of the circle and square also links a length of 29.53125 inches, corresponding to a lunation in days, to a square with sides of 2 metres.

We can also interpret the side of the Great Pyramid as √2/√3 x 100 000 / 354.36708 = 230.40983 metres, equivalent to 9071.2531 inches. A lunar year is 354.36708 days. An inch is 2.54 cm. The existence of the metre owes a lot to the number 254, in its role with the inch as "day-inch". A lunar year can be represented geometrically as 200 000 x √2 / (254 x π) = 354.45524, which basically means that 20 x √2 /π metres are very nearly equal to a lunar year in day-inches. This is especially interesting when 20 cm x 2.61803, which is Phi squared, make a royal Egyptian cubit, as 52.3606 cm (20.6144 inches), and also, if we were to add a value of 2.61803 cm to this cubit in cm, we would obtain a nice approximation of pi, 3.141636. Furthermore, if we were to multiply that cubit as a value in inches by the number of days in a lunar year and divide by 20, we would obtain a nice approximation of the solar year in days: 20.6144 x 354.36708 / 20 = 365.2534. This gives a strong indication that the metre and the inch are both intimately connected to the Giza plan, and to each other.

To multiply by 10 000 / 254 is very close to multiplying by 20 x √2 / (π x 354.36708), which means to convert inches to metres is very nearly equivalent to multiplying by 20 x √2 / (π x 354.36708). this suggests that the inch and the metre are connected to astronomy and geometry, specifically the moon, the square and the circle.

Notes

1.Le Gentil, Guillaume, Voyage dans les Mers de l'Inde,. Vol 1

2. Heath, Robin, & Michell, John, 2006. The Lost Science of Measuring the Earth, Adventures Unlimited Press

3. See Michell, J, 1972 City of Revelation: On the Proportions and Symbolic Numbers of the Cosmic Temple, Garnstone Press, and 1981 Ancient Metrology: the Dimensions of Stonehenge and of the Whole World as Therein Symbolized, Pentacle Books

4. Thom, A. (1961). The Geometry of Megalithic Man. The Mathematical Gazette, 45(352), 83–93. https://doi.org/10.2307/3614618

5. Heath, Richard, The Origins of Megalithic Astronomy as found at Le Manio