9. Sun Worship and Phi
- M Campbell
- Jul 20, 2019
- 55 min read
Updated: Mar 7, 2023

Phi, the Golden Ratio
What is Phi? It's a number close to 1.618. It's an irrational number, meaning that you can never fully write all the digits out, they go on forever. And it's also not a number.
At least, that's what John Anthony West says, in his Serpent in the Sky.
"Phi is not a number. It is a function." (p. 64)
What does he mean? Perhaps, simply, that its value is in its use, which is to multiply things. This could include sequences of numbers, linear measures, or angles.While it is an irrational number, in practice, an approximation has to be used, perhaps 1.618, or a fraction with a Fibonacci number for the nominator and denominator, such as 144/89, or 55/34, or for Phi squared, 2.618 or 144/55 for example. Whether Phi is considered as a number or not, it is its use as a ratio, in an applied way that matters. However, the fact that this ratio or number cannot be expressed exactly in a fractional or decimal form is also central to its importance. Perhaps for this reason it is associated with the ineffable, the divine.
Phi and its square can be calculated with the use of the square root of five, which is itself irrational:
(1 + √5 ) / 2 ≈ 1.618033988749894848204586834...
(3 + √5 ) / 2 ≈ 2.6180339887498948482045868343656
Phi is central to geometry. It is found in certain geometric shapes, most obviously the pentagon and pentagram, but also many other shapes can be made 'golden' to conform to a Phi ratio, for example, a golden rectangle or a golden triangle, or even a golden ellipse. It is almost incredible that two parts of a geometric shape can be linked by an irrational ratio. This is true for example of the side of a square and its relation to the square's diagonal. The length of this diagonal cannot be expressed exactly in its relation to the rest of the square, because the square root of two is irrational. The same goes for three dimensional shapes. The consequences of the central part irrational numbers play in Platonic solids, as well as intriangles, circles, squares, and pentagons, cubes and spheres, can be interpreted philosophically. As John Anthony West writes:
Phi, pi, and the square roots of two, three and five are all that are required to form all Perfect geometric solids, and to define and describe all possible harmonic combinations. It is the web of interaction, this vast complex of harmonies, that we respond to as 'the world' - in this case, the physical world, but which is but one (the tangible, perceivable) aspect of the spiritual world, or world of consciousness. The key to this harmonic world is number, and the means by which number is to be understood is geometry.
John Anthony West, Serpent in the Sky, p 64.

Phi (denoted below as φ )has some amazing properties. Two quantities a and b are said to be in the golden ratio φ if a + b / a = a / b = φ . These quantities may be lines, angles, areas of squares or circles. Or even quantities of time, as when you divide 24 hours into two parts, one the number of hours of daylight on a certain day, and the other part the number of hours of darkness.

If you divide a whole by phi, you are left with two parts: the greater part, a, is bigger than b by exactly the same multiple as the whole (a+b) is bigger than a. Since Phi is associated with life and growth, it may be more helpful to think of it as part of a multiplication rather than a division. If you take a quantity Q, and multiply it by φ, you get a new quantity S. The difference between Q and S is R, so Q + R = S. But also, curiously, this happens: R / φ = Q, S / φ = R, and Q x φ = S. And of course you can keep going. Take S and multiply it by φ : S x φ = U, U being a new amount, created by multiplying S by φ, and T the difference between S and U. The same thing happens: T / φ = S, U / φ = T, S + T = U.
Q is the smallest part, then R, then S, then T, then U.
Q + R = S, S + R = T, S + T = U
In this way you can create long sequences of numbers, or geometric shapes.
Another unique property of Phi is that it is the only number of which the square of the number is equal to the number plus 1.
Φ² = Φ + 1
1.618² = 2.618
1.618 + 1 = 2.618
And this leads to the fact that for any n:
Phi n+2 = Phi n+1 + Phi n
There are various number sequences formed by Phi, the most famous of which is the Fibonacci number sequence.
Starting with 0 and 1, each new number in the sequence is simply the sum of the previous two.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 . . . (Fibonacci himself started with 1 not 0)

Fibonacci was a 13th century Italian mathematician. His actual name was Leonardo of Pisa, or Leonardo Bonacci, the Fibonacci name was made up by a historian, 'Fi' simply standing for 'son of', just as in the tradition of adding the prefix "Fitz" to family names long ago, in the Norman tradition. Fibonacci is best known today for the number sequence that bears his name, but also crucially introduced the Hindu - Arabic number system to Europe, with the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 etc. As the Fibonacci number sequence was originally Indian in origin, from as early as the sixth century, it seems Fibonacci must have read about it in the same volumes of mathematics he discovered the number system in.
The ratio of each successive pair of numbers in the sequence approximates Phi (1.618. . .) , as 5 divided by 3 is 1.666…, and 8 divided by 5 is 1.60.
Fibonacci used it to show how it can describe growth in nature, with the example of rabbits reproducing, but he didn't make the connection himself to the golden ratio (which he also used, but independently). This was made later by a German mathematician called Simon Jacob, in the 16th century.
Below is a series of fractions made up of consecutive Fibonacci numbers:
3 / 2 = 1.5
5 / 3 = 1.66667
8 / 5 = 1.6
13 / 8 = 1.625
21 / 13 = 1.61538
34 / 21 = 1.61905
55 / 34 = 1.617647
These ratios progressively approach φ. After the 40th number in the sequence, the ratio is accurate to 15 decimal places. (1.618033988749895 . . .)
Fibonacci numbers in Pascal’s Triangle, developed by the French Mathematician Blaise Pascal, and formed by starting with an apex of 1.
Who knows when the golden ratio was first discovered and applied by mankind, perhaps many many thousands of years ago. Both pi and Phi feature in the design of the Great Pyramids, and Phi is in their layout too, as we'll see below.
Phi appears both the patterns of life and growth and in the proportions living creatures and plants. Here are just some of the things that are phi-structured:
DNA, the human body, from head to toe, but also in the face, especially in what are thought of as beautiful faces, in the hand, even in the rhythm of the heartbeat, a fertilized egg divides and multiplies in way in which the ratio of the succeeding number of cells to the previous number of cells is phi, population growth in cities is said to be phi related, stock exchange patterns too. Phi can be seen in the structure of insects, animals, plants, and other creatures.
Below is an image, taken from Gary Meisner's fantastic website https://www.goldennumber.net/.

The above image is from another great website: http://www.natures-word.com .The Spiral Movement of Leaf / Branch Distribution, "In an overwhelming number of plants, a given branch or leaf will grow out of the stem approximately 137.5 degrees around the stem relative to the prior branch. In other words, after a branch grows out of the plant, the plant grows up some amount and then sends out another branch rotated 137.5 degrees relative to the direction that the first branch grew out of." by Aidrian O'Connor.
Phi in the Ancient World
The golden ratio, but mathematically and historically, is endlessly fascinating.

In order to make sense of its history, Egypt beckons: it is one of the places where Phi controlled artefacts and structures have endured the best.
William Flinders Petrie
William Flinders Petrie was a British archaeologist and egyptologist. Born on June 3rd, 1853 in Charlton, Kent. At thirteen, he read Piazzi Smyth's Our Inheritance in the Great Pyramids, the author was apparently an acquaintance of his dad's. Petrie was primarily self-taught and had no formal schooling. At the age of eight, he was tutored in French, Latin, and Greek, until he had some kind of collapse, after which he was taught at home.
At the age of 19, he produced the most accurate survey of Stonehenge.
In 1880, at the age of 24, Flinders Petrie published his first book called Stonehenge: Plans, Description, and Theories; this book would become the basis for future discoveries at that site. That same year, he began his more than forty years of exploration and examination of Egypt and the Middle East.
For two years, while he worked at Giza, he lived in an old tomb in the rock.
I had a doorway in the middle into my living room, a window on one side for my bedroom, and another window opposite for a store-room. I resided here for a great part of two years; and often when in draughty houses, or chilly tents, I have wished myself back in my tomb. No place is so equable in heat and cold, as a room cut out in solid rock; it seems as good as a fire is in cold weather, and deliciously cool in the heat.
I settled at Gizeh in December, 1880, and lived there till the end of May, 1881; I returned thither in the middle of October that year, and (excepting two months up the Nile, and a fortnight elsewhere), lived on there till the end of April, 1882; thus spending nine months at Gizeh. Excellent accommodation was to be had in a rock-hewn tomb, or rather three tombs joined together, formerly used by Mr. Waynman Dixon, C.E.; his door and shutters I strengthened; and fitting up shelves and a hammock bedstead, I found the place as convenient as anything that could be wished. The tombs were sheltered from the strong and hot south-west winds, and preserved an admirably uniform temperature; not varying beyond 58º to 64º F. during the winter, and only reaching 80º during three days of hot wind, which was at 96º to 100º outside.
The Pyramids and Temples of Gizeh, Flinders Petrie

He had travelled to the Pyramids at Giza in 1880 to survey them, understand their geometry and properly investigate how they were constructed, and he was the first person in modern times to do so, using first hand observation.
After Giza, Flinders Petrie explored and excavated over thirty sites in the Middle East. One of his most famous finds was a Stele of Mernepath at Thebes which contains the earliest known Egyptian references to Israel. One of his trainees, Howard Carter, discovered the tomb of Tutankhamun in 1922. In 1923 he was knighted for services to British archaeology and Egyptology. In 1927, Flinders Petrie returned to Palestine uncovering ruins and remained there until his death at the age of eighty-nine, in Jerusalem on July 28, 1942.
How to measure a pyramid

The orientation of the pyramids is a good place to start, if only because it gives an indication of the precision of the architect's and builders' work.
It is worth quoting Flinders Petrie at length here:
93. The orientation of the Great Pyramid is about 4' West of North; a difference very perceptible, and so much larger than the errors of setting out the form (which average 12"), that such a divergence might be wondered at. When, however, it is seen that the passage, which was probably set out by a different observation, nearly agrees in this divergence, it seems unlikely to be a mere mistake. And when, further, the Second Pyramid sides, and also its passages, all diverge similarly to the W. of North, the presumption of some change in the position of the North point itself, seems strongly indicated. The Third and lesser Pyramids are so inferior in work, that they ought not to interfere with the determination from the accurate remains; they would, however, scarcely affect the mean deviation if included with the better data. The azimuths of the two large Pyramids are thus:—
Great Pyramid, casing sides Great Pyramid, core sides – 5' 16" ± 10" Second Pyramid, casing sides – 5' 26" ± 16" Second Pyramid, passage (Smyth) – 5' 37" ± 10" ? Great Pyramid, passage (Smyth) – 5' 49" ± 7" – 3' 43" ± 6"
[p. 126] In considering these results, the difference of the casing and core azimuths of the Great Pyramid shows that probably a re-determination of the N. was made after the core was finished; and it must be remembered that the orientation would be far more difficult to fix after, than during, the construction; as a high face of masonry, for a plumb-line, would not be available. The passages of the Great and Second Pyramids are the most valuable elements; as, being so nearly at the polar altitude; a very short plumb-line would transfer the observations to the fixed plane. Considering, then, that the Great Pyramid core agrees with the passages far closer than does the casing, the inference seems to be that the casing was fixed by a re-determination of N., by the men who finished the building. These men had not the facilities of the earlier workers; and are shown, by the inferiority of the later work in the Pyramid, to have been far less careful. Hence the casing may probably be left out of consideration, in view of the close agreement of the four other determinations, one of which — the passage — was laid out by the most skilful workmen of the Great Pyramid, with their utmost regularity, the mean variation of the built part being but 1/50 inch.
The simple mean of the last four data is – 5' 32" ± 6"; their divergences being just what would be expected from their intrinsic probable errors. The passages are, however, probably far the most accurate lines in their execution and as the Second Pyramid is inferior in its workmanship, – 5' 45" ± 5" might be well taken as the result from them alone. On the whole, considering the various values of the data, – 5' 40" ± 10" may be taken as a safe statement of the suggested place of the pole, at the epoch of the Pyramid builders.
William Flinders Petrie, The Pyramids and Temples of Gizeh
In other words the workmanship and planning of the Great Pyramid is so precise that Flinders Petrie wonders at a divergence of just a few seconds of degree from north. This same divergence is found both inside and outside the structure.
Flinders Petrie briefly discusses the possibility of a change in the axis of the earth, and reckons that, going by the pattern of change in recent centuries, the difference in the orientation of North 4,000 to 6,000 years ago should only be about one minute. However, the orientation of the Great Pyramid is about 5 minutes West of North. Either something happened to change the axis abruptly, or if the change in the axis was gradual, the pyramids are much older than 6,000 years. Flinders Petrie ponders on the possibility of ocean currents tugging at the polar axis.

It's hard to imagine exactly how difficult it must have been to start measuring the pyramids. When Flinders Petrie got there, they were surrounded by sand, broken casing stones, and some precarious large blocks weighing a ton or more. He had to figure out where the pyramid began and where it ended, which parts were still buried, what might once have been.
From these extracts you can get an idea of the challenges he faced:
[p. 45] The limestone pavement was found on the N. side first by Howard Vyse, having a maximum remaining width of 402 inches; but the edge of this part is broken and irregular, and there is mortar on the rock beyond it, showing that it has extended further. On examination I found the edge of the rock-cut bed in which it was laid, and was able to trace it in many parts. At no part has the paving been found complete up to the edge of its bed or socket, and it is not certain, therefore, how closely it fitted into it; perhaps there was a margin, as around the casing stones in the corner sockets.
28. The basalt pavement is a magnificent work, which covered more than a third of an acre. The blocks of basalt are all sawn and fitted together; they are laid upon a bed of limestone, which is of such a fine quality that the Arabs lately destroyed a large part of the work to extract the limestone for burning. I was assured that the limestone invariably occurs under every block, even though in only a thin layer. Only about a quarter of this pavement remains in situ, and none of it around the edges; the position of it can therefore only be settled by the edge of the rock-cut bed of it. This bed was traced by excavating around its N., E., and S. sides; but on the inner side, next to the Pyramid, no edge could be found; and considering how near it approached to the normal edge of the limestone pavement, and that it is within two inches of the same level as that, it seems most probable that it joined it, and hence the lack of any termination of its bed.
Flinders Petrie was able to determine the length of the sides, and then measure the angle of the sides against the ground, to determine the true original height. You can see from the photo below, from the mid to late 19th century, that there was a lot of sand around the pyramid complex in the time Flinders Petrie was there.

Here are some of the results Flinders Petrie came up with, all in inches:
On the whole, we probably cannot do better than take 51º 52' ± 2' as the nearest approximation to the mean angle of the Pyramid, allowing some weight to the South side.
The mean base being 9068.8 ± .5 inches, this yields a height of 5776.0 ± 7.0 inches."
"This square, of the original base of the Great Pyramid casing on the platform, is of these dimensions:—
N 9069.4 E 9067.7 S 9069.5 W 9068.6"
"Level of the King's Chamber is where the Pyramid diagonal equals the base side. Diagonal of passage section (vertical) rises parallel to the Pyramid face 51º 52' Diagonal of inside end of coffer rises parallel to the Pyramid face 51º 52'. Diagonal of inside bottom of coffer is double its height, or 4 cubits. Diagonal of floor of King's Chamber is double its height."
"Angle of casing as measured By theory of 34 slope to 21 base 51º 52' ± 2'"
"On the whole, we probably cannot do better than take 51º 52' ± 2' as the nearest approximation to the mean angle of the Pyramid, allowing some weight to the South side.
The mean base being 9068.8 ± .5 inches, this yields a height of 5776.0 ± 7.0 inches."
"41. In the Queen's Chamber it seems, from the foregoing statement, that the ridge of the roof is exactly in the mid-place of the Pyramid, equidistant from N. and S. sides; it only varies from this plane by a less amount than the probable error of the determination.
The size of the chamber (after allowing suitably in each part for the incrustation of salt) is on an average 205.85 wide, and 226.47 long, 184.47 high on N. and S. walls, and 245.1 high to the top of the roof ridge on E. and W. walls. "
" Wide High
King's Chamber, mean dimensions 206.13 235.2 or 5 x 41.22 and 47.04 Gallery, lower part, vertically 82.42 92.4 to 94.6 2 x 41.21 and 46.2 to 47.3 Passages 40.6 to 42.6 46.2 to 48.6 40.6 to 42.6 and 46.2 to 48.6 Ramps of gallery, vertically 19.3 to 20.4 22.65 to 23.76 ½ x 38.6 to 40.8 and 45.3 to 47.5 Width 206.12 ± .12 squared, is 100 cubits of 20.612 ± .012 Length 412.24 ± .12 squared, is 400 cubits of 20.612 ± .006 Height 230.09 ± .15 squared, is 125 cubits of 20.580 ± .014
"Level of the King's Chamber is where the Pyramid diagonal equals the base side. Diagonal of passage section (vertical) rises parallel to the Pyramid face 51º 52' Diagonal of inside end of coffer rises parallel to the Pyramid face 51º 52'. Diagonal of inside bottom of coffer is double its height, or 4 cubits. Diagonal of floor of King's Chamber is double its height.
His measurements are still considered perfectly accurate, despite all that sand and rubble he had to deal with. I also use the most recent survey of the Great Pyramid by Glen Dash but there is much less data and it's much less precise, measured in metres to only three decimal points. Here is a link to the recent survey of the Great Pyramid
The layout of the Pyramids on the ground is interesting. Perhaps it is the most interesting part, especially since Robert Bauval's insights - that the layout of the pyramids matches the layout of the three stars of the belt of the constellation Orion, a constellation associated with one of the main figure heads of the ancient Egyptian religion: Osiris. Until then Flinders Petrie's view had prevailed, that there was no particular method to the planning of the ground layout of the pyramids. Here is another extract from Flinders Petrie's book The Pyramids and Temples of Gizeh, on the ground layout:
"92. [p. 125] The relative positions of the three larger Pyramids to one another were completely fixed in the triangulation, which included them all. The following are their distances apart, as measured on parallels inclined – 5' to true N.— i.e., at the mean azimuth of the First and Second Pyramids; and also the distances, and the angles from these parallels, of the direct lines from one Pyramid to another:—
N E Direct
Centre of First to centre of Second Pyramid 13931.6 and 13165.8 = 19168.4 at 43º 22' 52" Centre of First to centre of Third Pyramid 29102.0 and 22616.0 = 36857.7 at 37º 51' 6" Centre of Second to centre of Third Pyramid 15170.4 and 9450.2 = 17873.2 at 34º 10' 11"
There does not appear to be any exact relation between their centres, or between the corners; and from the nature and appearance of the ground, and the irregularity of the peribolus walls, it would not seem likely that any connection had been planned.
(Italics my own)
The Great Pyramid is a golden pyramid
Glen Dash gives a mean average side of 230.363 metres, which works out at 9069.4 inches. Though Flinders Petrie's figures, are slightly different, they are much more precise. He gives a mean value of 9,068.8 inches ± 0.5 for each base side, or 755.7333 feet.
(However when he was writing the inch was a little different to today's inch, as it was standardised to the metre in a new way. Flinders Petrie was working with a 39·370113 inch metre and today the metre is valued in inches as 39.3700787402 inches. So arguably you could re-evaluate his 9068.8 inch figure accordingly to 9,068.79 inches.)
If the cubit is 20.62 inches (0.5237 meters) according to Flinders Petrie, the average base length is 439.806 cubits according to Flinders Petrie's measurements or 439.8351 cubits according to the most recent survey. Flinders Petrie varies the value of the cubit though, sometimes 20.632 inches, sometimes 20.612 inches, sometimes 20.580, depending on the area he is measuring, and as he tries to make sense of the figures in cubits. If you use the cubit value of 20.612 inches, the base side is 440.0058 cubits long.
For the height, Flinders Petrie has 5776.0 ± 7.0 inches, which is 481.3333 feet, or 146.71039 metres, or 280.1163 cubits of 20.62 inches, or 280.2251 cubits of 20.612 inches. This he works out with the value of the mean angle of the slope of the pyramid of 51º 52' ± 2'. (or 51.8667º ± 0.0333º).
What's the ratio between base and height?
Working in inches:
5,776 / 9,068.8 = 0.6369
9,068.8 / 5,776 = 1.5701
1.5701 is close to half of pi, and 0.6369 is close to what you would expect the ratio of height and base in a golden pyramid to be.
Curiously, no mention is made of Phi by Flinders Petrie in this book by the way. Using Flinders Petrie's figures in inches:

The base length 9068.8 divided by 2 is 4,534.4. So half the base length is 4,534.4 inches.
The slant height can be calculated as 7,343.2 inches.
This divided by half the base side is 1.61944, a figure close to φ.
The slant height divided by Phi would be 4,538.358 inches. That's a difference of just under 4 inches to the actual half base length.
The square root of 1.61803 is 1.272018. The ratio of pyramid height to half the base length should match this.
The height 5776.0 divided by 1.272018 is 4,540.816. That's a difference of 6.416 inches from the actual half base.
If we allow for these differences of 4 and 6 inches approximately between the actual half base length and the ideal phi engineered half base length, then we can safely say that the Great Pyramid is a golden pyramid. Half the base length being in fact 4,534.4 inches long, this amounts to a difference of between 0.0882% and 0.1415%.
What about areas? You would expect them to be in Phi ratio too.
What is the area of each face of the pyramid? It is found by multiplying the base side by the slant height and dividing by 2. The average base length is 9,068.8 inches, which gives a base area of 82,243,133.44 in². This times the slant height of 7,343.23 in and divided by 2 gives a value of 33,297,459.52 in² per side, or face of the pyramid, and a total of 133,189,838.08 for all 4 sides. 133,189,838.08 divided by 82,243,133.44 is 1.61946, very close to φ. 133,189,838.08 divided by φ is 82,316,049.814, a difference of 72,916.373 in² between this and the actual base area.
All this means that the Great Pyramid has a base surface area in φ ratio to its sides surface area, and that the slant height is in φ ratio to half the base length.
A Piece of π
Taking the Glen Dash figure for the base side of the pyramid of 230.363 m, and a height of 146.71039 m, this link between the base and height of the ratio becomes apparent in metres:
2 x base side - height = 314.01561
This is close to 10 x pi. Was this intentional?
In metres, (base / 2) + height = (230.363 / 2) + 146.71039 = 262.02539, which is very close to φ² x 100 = 261.8021. Phi is, to an error of 2.518 cm, linked to the dimension in metres of height and half base, added together. These two observations are from Patrice Pooyard's film The Revelation of the Pyramids.
The Great Pyramid embodies spherical properties: it's base sides combine to form a measure that is (almost) in pi ratio with its height, just as a circumference of a circle is in pi ratio to its radius.
base side x 4 ≈ height x π x 2
or: base side x 2 ≈ height x π
The average base length is 9,068.8 inches, which times four makes 36,275.2 inches, or 3,022.933 feet (according to Flinders Petrie's figures). For the height, Flinders Petrie has 5,776.0 ± 7.0 inches, which is 481.3333 feet.
Taking π as 3.1416, we get: 5,776 x 3.1416 x 2 = 36,291.7632, which converts to 3,024.3136 feet.
This is 16.5632 inches greater than the four average base lengths added together - the difference between an exact π height to base perimeter ratio and the actual base perimeter is just over 16 inches.
9,068.8 x 2 / 3.1416 = 5773.36389
This is 2.63611 inches less than the actual height.
If we take Flinders Petrie's value for the south face base side, the greatest of them, at 9,069.5 inches, this difference between pi projected value and actual value of the height in inches is even smaller.
9,069.5 x 2 / 3.1416 = 5,773.809
(only 2.1905 inches difference with 5,776).
Using the most recent base side figure by Glen Dash of 9,069.4 inches, this gives 5,773.74586, a difference of 2.2541 inches with 5,776.
The slant height of 7,323.2 inches can also be included here.
5,776 x 4 / 7343.2 = 3.14631
5,776 x 4 / 3.1416 = 7,354.21441
With an error of 11 inches, height and slant height are related to each other by 4π.
The Pyramid of the Sun at Teotihuacan in Mexico also expresses this pi ratio, as Graham Hancock wrote about:
(...) the original height of the monument (481.3949 feet), and the perimeter of its base (3023.16 feet), stood in the same ratio to each other as did the radius of a sphere to its circumference. This ratio was 2pi (2 x 3.14) and to express it the builders had been obliged to specify the tricky and idiosyncratic angle of 52 for the pyramid's sides (since any greater or lesser slope would have meant a different height-to-perimeter ratio).
(...) the so-called Pyramid of the Sun at Teotihuacan in Mexico also expressed knowledge and deliberate use of the transcendental number pi; in its case the height (233.5 feet) stood in a relationship of 4pi to the perimeter of its base (2932.76 feet).
Fingerprints of the Gods, by Graham Hancock, Kindle Loc 5957 45%
Graham Hancock quotes Livio Stecchini from Secrets of the Great Pyramid:
The Great Pyramid was a projection on four triangular surfaces. The apex represented the pole and the perimeter represented the equator. This is the reason why the perimeter is in relation 2pi to the height.
Fingerprints of the Gods, by Graham Hancock, Kindle Loc 7990 60%
And what is the ratio between the size of the Great Pyramid and the size of the Northern Hemisphere?
Graham Hancock uses the best modern figure of 24,902.45 miles (131,484,936 feet) for the equatorial circumference, and the polar radius of 3,949.921 miles (20,855,582.88 feet).
The pyramid base perimeter is, with Flinders Petrie's measurements, 9,068.8 x 4 = 36,275.2 inches (3,022.93212 feet), or with Glen Dash's measurements 9069.4094 x 4 = 36,277.6378 inches, (3,023.1352 feet).
131,484,936 / 3,022.933 = 43,495.8155
131,484,936 / 3,023.1352 = 43,492.9063
Average: 43,494.3609
The scale used for the base perimeter is: 1 : 43,494.3609
The pyramid height is 5,776.0 feet. If the height to base ratio were exactly π in the Great Pyramid, then taking the height as 5,776, the perimeter base would be 3,024.3136 feet, as we saw above. If we divide the circumference of the Earth in feet by this figure, we get: 131,484,936 / 3,024.3136 = 43,475.9596.
Alternatively, you could use a value of 24,883 miles for the equatorial circumference, used by Robin Heath in his book The Lost Science of Measuring the Earth, which appears to be an ancient value. This then gives a scale of 1:43,461.843
Why is the π ratio not exact in the pyramid? Is it because the Earth is not in fact a precise sphere, but bulges at the equator and is flatter at the poles? There is, it's true, a difference of 16 inches between what would be the base perimeter of the Great Pyramid if it were exactly in pi ratio to its height, and the actual base perimeter. However, the actual pyramid measurements are 16 and a half inches smaller than a perfect π height to base ratio, to bigger, and so cannot reflect an equatorial bulge.
What about the scale used then to represent the Earth in this Great Pyramid? It seems to be 1 : 43,494.3609 or 1:43,461.843 .
Graham Hancock shaves a bit off this 43,495.8155 number to approach 43,200.
What's the significance of 43,200?
It's probably best to go back to an earlier section of Fingerprints, where Graham Hancock quotes Giorgio de Santillana from Hamlet's Mill, and mention the concept of precession.
During the course of each year the earth's movement along its orbit causes the stellar background against which the sun is seen to rise to change from month to month: (...) At present, on the vernal equinox, the sun rises due east between Pisces and Aquarius. The effect of precession is to cause the 'vernal point' to be reached fractionally earlier in the orbit each year with the result that it very gradually shifts through all 12 houses of the zodiac, spending 2160 years 'in' each sign and making a complete circuit in 25,920 years.
Quoted in Fingerprints of the Gods, Kindle Loc 4597, 34%
The key here is 25,920 years. This is one Great Year, one big circle travelled by the sun. And 10 / 6 of 25,920 is 43,200.
The scale used to determine the height and base of the Great Pyramid is linked to a cycle of the sun, or at least, to 10 / 6 of one: precession - if you are happy to accept that 43,495.8155 is close enough to 43,200. It's not a perfect fit.
But this is weird. The equatorial circumference of the earth in miles divided by 108, a precessional number, gives a value close to the base of one side of the Great Pyramid in metres (230.34751 metres). The ancient value for the equatorial circumference is 24,883.2 miles, according to Robin Heath and John Michell in The Lost Science of Measuring the Earth, which is a little short of the current estimate of 24,901.461 miles, according to Wikipedia. The equatorial circumference divided by 27 gives a value close to the base circumference of the Great Pyramid, 921.39004 metres, according to Flinders Petrie's measurements, converted from inches.
24,883.2 / 108 = 230.4
24,883.2 / 27 = 921.6
24,901.461 / 108 = 230.569
24,901.461 / 27 = 922.2763
This doesn't work quite as well with the ratio between pyramid height and Earth polar radius. The height of the pyramid is 146.5 metres according to Wikipedia and 146.71039 metres according to Flinders Petrie, the polar radius is 3,950 miles, according to Wikipedia, and the ancient value is 3,949 5/7 miles.
3950 / 27 = 146.2963
146.28571 / 27 = 146.2857
3,949.7142857 / 146.71039 = 26.9218
With this in mind, you could begin to think of pi as linked to the sun too, together with Phi.

Pi and Phi as Easy Bedfellows
How can a geometric structure embody both φ and π? How do they get along?
The Great Pyramid's outer structure has a height to base perimeter ratio close to π.
base side x 2 ≈ height x π
It is also a golden pyramid in that it has a base surface area in φ ratio to its sides surface area, and that the slant height is in φ ratio to half the base perimeter.
The slant height of the pyramid divided by the height is: 7,323.2 / 5,776 = 1.27133, which multiplied by 3.1416 gives 3.99401.
The slant height of the pyramid divided by the square root of phi is:
7,323.2 / √ 1.618 = 5,757.15087
5,776 - 5,757.15087 = 18.84913
slant height √ φ ≈ height
In a golden pyramid you would expect to find half the base to be in phi ratio to its slant height, and the height is the square root of phi of this slant height.
The average value of a base side is 9068.8 inches. Half the base side times phi gives 7,336.6592, which is close to the value of the slant height in inches. This number divided by the square root of phi gives 5,767.78532.
9068.8 / 2 x 1.618 = 7,336.6592
7,336.6592 / √ 1.618 = 5,767.78532
base side / 2 x φ ≈ slant height
The slant height is in fact 7,343.2 inches, and the pyramid height is 5,776 inches, differing from the above calculations by 6.5408 inches and 8.21468 inches respectively. Height and slant height are related by √ 1.618 with an error of about 8 inches.
Also we've seen that, with an error of 11 inches, height and slant height are related to each other by 4/π. (5,776 x 4 / 3.1416 = 7,354.21441)
slant height ≈ height x 4 / π ≈ height x √ φ
√ φ x π =3.9961
Pi and the square root of Phi are bound by a number close to 4. If you wanted to represent Earth using pi and phi you could do worse than to build a four sided structure. Is it because these two irrational numbers are only very approximately connected in this way that neither pi nor phi can be exactly measured out in the Great Pyramid, allowing, as it must, for both functions to work imperfectly together? I thought at first that maybe any discrepancies between exact Phi and pi ratios and the actual dimensions of the pyramid might be down to pi and phi being uneasy bedfellows, that you couldn't achieve precision with one without botching the other. But in fact, applied pi and applied phi are surprisingly respectful of each other. Any inaccuracies caused by them both living under (or in) the same roof must be dismissed as meaningless, because the slight errors in their applications have produced a pyramid that is bigger than both an ideal pyramid with exact pi ratio, and one with an exact phi ratio, not somewhere between the two. In any case, the errors that do exist are between 6 and 11 inches on a massive structure.
Not only that, but William Flinders Petrie gives his figures room for error: he specifically says the mean base is 9068.8 ± 0.5 inches, which yields a height of 5776.0 ± 7.0 inches, so a difference of 14 inches or so in the pi and Phi ideal pyramid dimensions is well within the limit.
We've seen that if we multiply the base side by 2 pi, we get a figure for the height which is slightly too small compared to the actual height, by 2.63611 inches. And if we multiply the half base side by phi we get a height which is slightly too small by 8.21468 inches. Both of these differences are tiny, but it seems that, of the two, pi is more precisely adhered to in the outer construction of the Great Pyramid.
Why do pi and Phi get along so well? They do very different things, but they are linked in several ways.
3.1416 x 5 / 6 = 2.618
1.618² = 2.618
Because pi and Phi are infinitely long numbers, this link between them is not exact and mathematicians might protest that it's not even correct. But it's true to say that if you use approximations of pi as 3.1416 and phi as 1.618 then pi x 5/6 = phi²
Also, by chance, the square root of Phi and pi divided by four are quite similar:
√φ = 1.272018
4/π = 1.27324
And as it happens, these two figures both (imperfectly) define the height of the pyramid in relation to half its base.
This is possibly the single best reason why pi and Phi work together so well in the Great Pyramid, or in any pyramid: where either is used to define the the height in relation to half the base, the other will foll
Below is a diagram I have made of three triangles, all cross sections of pyramids through their centres. The first shows a height to base ratio according to Phi, the second according to pi, and the third shows the actual ratios in the Great Pyramid.ow.
The Great Pyramid's mean base side is 9,068.8 inches, the mean angle of the slop of the pyramid is 51.8667°, the mean base side is 5,776 inches, according to the Flinders Petrie figures. The height divided by half the base side gives a ratio of 1.27381. Curiously, you can see from the figures in the diagram that the Great Pyramid could embody pi and phi more closely still. It's height to base ratio is not somewhere between a pefect Phi ratio and a perfect pi ratio, its ratio is not a mean of pi and Phi ratios, but outside of both. A pyramid with a base of 9,068.8 has a half base of 4,534.4, and this times √φ gives 5,767.8388, and times 4/π the half base is 5,773.3639. The height of the Great Pyramid being 5,776, you can see that a height according to either pi or Phi ratios of base to height would be slightly shorter than the actual height.

If you take a square which contains a circle exactly within its sides, so that the diameter of the circle is the same as a side of the square, and if the radius has a value of 1 and a side of a square has a value of 2, the area of the square has a value of 4, and the area of the circle is π. The 4/π ratio is found in the Great Pyramid, in that the height is half the base of the pyramid x 4 / π.

If you take a circle 1 unit in diameter, calculate the circumference, and divide it by 6, you get: 0.5236
If you take pi and subtract phi² from it you get: 3.1416 - 2.618 = 0.5236
To four decimal places, the results are the same.
Were the pyramid builders aware of this?
The value of a royal cubit is 0.5236 metres.
You can decide whether to believe this proves nothing, because the pyramid builders could not have known about pi, Phi or the metre, as most historians believe, or that it shows that the builders of the pyramids not only knew about this correlation between pi and Phi but also about the metre.
Phi and pi get along easily. Another question you might ask is why do the inch, cubit and metre get along so well inside this Great Pyramid?
Inside the Great Pyramid
The golden ratio is also to be found inside the Great Pyramid.
The Queen's Chamber. Measurements taken from Flinders Petrie's The Pyramids and Temples of Gizeh.
"The size of the chamber (after allowing suitably in each part for the incrustation of salt) is on an average 205.85 wide, and 226.47 long, 184.47 high on N. and S. walls, and 245.1 high to the top of the roof ridge on E. and W. walls."
With the Queen's Chamber 205.85 wide, and 226.47 long, the perimeter is 864.64 inches.
864 is a very important symbolic number. In fact, John Michell calls it "the Foundation Number" (in The Dimensions of Paradise p. 194)
"An image of 864 is the rock at the center of the earth holding down the waters of the abyss, which is symbolized by the foundation or cornerstone of a temple and its altar."
John Michell points out that the diameter of the sun measures 864,000 miles, that there are 86,400 seconds in a day, that for Brahma one day and one night are 8,640 million years, and mentions various instances of this number used symbolically in architecture and in language (gematria).
864.64 is almost exactly 24 x 36. It is also (imperfectly) linked to phi: 864.64 / 7 x 1.618 = 199.855. This is very close to 200.
200 / 1.618 x 7 = 865.2657. This is less than an inch more than the actual perimeter.
If you take 864 and divide it by 7 you get 123.42857, which is the number of miles between Stonehenge and Lundy, or one side of Robin Heath's Lunation Triangle.
In metres, the width is 5.22859 m, length is 5.752338 m, 4.685538 m high on N. and S. walls, and 6.22554 m high to the top of the roof ridge on E. and W. walls.

The base width of the King's Chamber was found to be 206.16" (W) / 206.43" (E) inches by Flinders Petrie. The base length of the King's Chamber is 412.78" (N) / 412.53" (S), and the height is 230.09 inches. The mean lengths are: North, 412.4, East: 206.20, South: 412.11, West: 205.97. The sum of these mean values is 1236.77, which is close to 2,000/1.61803. (it's off by just over an inch) The added mean lengths of width and length combine to give a value of 412.4 + 206.97 = 619.37. This is close to 1,000 divided by Phi. Divide this by 1.618 and you get two segments, one of 382.7998 inches, and the other of 236.5814 inches. The mean values of North length, East width and South length, added together and multiplied by 0.2 give the base width of the West width, 206.16". The mean values of N and W combine to make 618.37".
To a couple of inches error, using the mean values, width + length ≈ 1,000 / φ
Using mean values for N and W, width + length + (width + length)/ φ = 1,000.55
(width + length + (width + length)/ φ)) / φ ≈ width + length
And since width = length / 2
width = ((width + length + (width + length)/ φ)) / φ ) / 3
The value of the cubit is therefore very close to ((width + length + (width + length)/ φ)) / φ ) / 30 inches.
or 1,000 / 30φ inches, and the width of the chamber is therefore 1,000 / (3 φ) inches.
Also, half of the floor width, 103.06 inches, plus the value of the height in inches, 230.09, makes 333.15, very close to one third of 1,000.
Also, 206.12 x 1.618 = 333.50216
So the combined values of the height and half the floor width make a figure close to the value of the width of the floor in inches multiplied by Phi.
That means that if you were to draw a line of 333.15 inches along the longer wall, adjacent to the length of the chamber, from floor to ceiling, the remainder would come to precisely the middle of the floor. 333.50216 - 230.09 = 103.06, and 103.06 is exactly half of 206.12 inches, the width of the King's Chamber.
Also, "Probably the base of the chamber was the part most carefully adjusted and set out; and hence the original value of the cubit used can be most accurately recovered from that part. The four sides there yield a mean value of 20.632 ± .004, and this is certainly the best determination of the cubit that we can hope for from the Great Pyramid." (The Pyramids and Temples of Gizeh).
So 333.50216 is close to 10 cubits squared. 20.632 x 1.618 x 10 = 333.82576
Another number close to 333.50216 is the product of the number of days in a lunation divided by phi and then squared. (29.53059 x 1.618)² = 333.1096
Another similar number 333.5376 can also be arrived at in this way: the number of days in a year divided by the number of days in 12 lunations x 200, which is 206.14190084. Multiply this by Phi and you get 333.537.
Another intriguing link between Phi and the cubit is this: If the cubit is taken as 20.626 inches, this is also equal to 19.008 + 1.618 inches. 1.618 is Phi, and 19.008 is another important number because divided by 6 it gives 3.168, the number found in many sacred structures. Also, divided by 7, 19.008 gives the value of an Astronomical Megalithic Yard in inches: 2.71542857. This last number is also arrived at in this way: The number of days in a year, 365.242199, minus the number of days in 12 lunations, 354.36708, is 10.875119. One lunation divided by this number is 2.7154268.
In metres the Kings Chamber's dimensions are:
width 5.235448 m, length 10.470896 m, height 5.844286 m.
(Length x 2 + width)/ φ x 10 = 1.619052
This is an observation made in The Revelation of the Pyramids.
"Probably the base of the chamber was the part most carefully adjusted and set out; and hence the original value of the cubit used can be most accurately recovered from that part. The four sides there yield a mean value of 20.632 ± .004, and this is certainly the best determination of the cubit that we can hope for from the Great Pyramid." (The Pyramids and Temples of Gizeh).
So 333.50216 is close to 10 cubits squared. 20.632 x 1.618 x 10 = 333.82576
Another number close to 333.50216 is the product of the number of days in a lunation divided by phi and then squared. (29.53059 x 1.618)² = 333.1096
Another similar number 333.5376 can also be arrived at in this way: the number of days in a year divided by the number of days in 12 lunations x 200, which is 206.14190084. Multiply this by phi and you get 333.537. (See the chart above)
I think there must be a link between the value of the cubit in inches, the dimensions of the King's Chamber, the ratios used in the Great Pyramid more generally (phi and pi), the distance in miles between the Michael Mounts, and the sun and moon cycles. If the cubit is used in the Great Pyramid, and if the cubit is derived from the lunar and solar cycles, together with the inch, then it stands to reason that the pyramid encodes lunar and solar cycles, or at least, their relationship with one another.
Another intriguing link between Phi and the cubit is this: If the cubit is taken as 20.626 inches, this is also equal to 19.008 + 1.618 inches. 1.618 is Phi, and 19.008 is another important number because divided by 6 it gives 3.168, the number found in many sacred structures. Also, divided by 7, 19.008 gives the value of an Astronomical Megalithic Yard in inches: 2.71542857. This last number is also arrived at in this way: The number of days in a year, 365.242199, minus the number of days in 12 lunations, 354.36708, is 10.875119. One lunation divided by this number is 2.7154268.
In metres the Kings Chamber's dimensions are:
width 5.235448 m, length 10.470896 m, height 5.844286 m.
In metres the Kings Chamber's dimensions are: (Length x 2 + width)/ φ x 10 = 1.619052
This is an observation made in The Revelation of the Pyramids.
The Second Pyramid
Below are Flinders Petrie's measurements of the base of the second pyramid:
" Length Diff from mean Azimuth Diff from mean
N. side 8471.9 – 3.0 inches – 5' 31" – 5"
E. side 8475.2 + 0.3 inches – 6' 13" – 47"
S. side 8476.9 + 2.0 inches – 5' 40" – 14"
W. side 8475.5 + 0.6 inches – 4' 21" + 65"
Mean 8474.9 1.5 - 5' 26" 33" "
67. For the angle of slope of the faces, the direct measures by goniometer and level on the granite in situ gave 53º 12' ± 2', but by measurement from plumb line 53º 2'; the block has been slightly shifted, but the top surface only varies 1' from level, being high on the outer edge. By goniometer measures of [p. 98] 24 blocks, both of granite and limestone, lying around the Pyramid, the mean is 53º 14' ± 5'; and though this involves the assumption of horizontal courses, if this be taken as the angle of slope, yet it agrees so closely with the casing in that probably 53º 10' ± 4' will be the best statement.
Hence the height will be 5,664 ± 13 inches.
In metres, the base side converts to 215.26246 metres ± 0.0381 and the height 143.8656 ± 0.3302.
The base of this pyramid, 8474.9 inches, divided by half the height (5,664 / 2) is close to 3. A triangle with one side worth half the base, the other the height of the pyramid, and the third the slant height, to represent half a cross-section of the pyramid through the centre, is basically a 3, 4, 5 triangle.
If the value taken for the height were slightly smaller, by just under a quarter of an inch, well within the margin of error, the total area of a cross section through the middle of the pyramid would be 24,000,000 square inches, or 2,000,000 square feet. As it is, with a height of 5,664, the area is 24,000,916.8 inches.
159. The Second Pyramid has not been theorized on to any large extent.
(...)
"Taking the great central chamber as the best wrought part of the inside, it is evident that the height of the sides is 10 cubits, being 206.4; but the breadth, 195.8, seems inexplicable, as 9½ cubits is not a likely quantity. In the Great Pyramid we have seen that all the dimensions of the chambers are explainable on the theory of the squares of the lengths being a round number of square cubits. Applying this theory to the Second Pyramid chamber, the
Wall height 206.4 squared = 100 square cubits of 20.640 End height 244.4 squared = 140 square cubits of 20.656 Breadth 195.85 squared = 90 square cubits of 20.644 Length W. from door 412.75 squared = 400 square cubits of 20.637 Length E. from door 144.9 squared = 50 square cubits of 20.493
The exactitude of the connection of theory and measurement here is remarkable; the only perceptible difference being in the length from the W. side of the doorway to the E. wall. And the value of the cubit required by the dimensions, 20.64, is extremely close to the cubit as best shown in the King's Chamber, 20.632 ± .004. If any objection be made to dividing the lengths into two parts, it should be noted that it is certainly so divided in the chamber, by the fact of the length of one part, 412.75, being exactly 20 cubits; the wall W. of the door being a double square, 10 x 20 cubits, equal to the floor of the King's Chamber.
The design of the squares of the dimensions, direct and diagonal, being in round numbers of square cubits, appears then to have been employed in this chamber, as in those of the Great Pyramid.
The rudely-worked lower chamber seems to have been simply designed in cubits. The length 411.6 being evidently 20 cubits of 20.58; and the breadth, 123.4, three times the passage breadth, or 6 cubits of 20.57. The recess opposite the entrance to this chamber is 122.0 to 123.8 long, apparently equal to the chamber breadth.
Both passages quoted from Flinders Petrie's The Pyramids and Temples of Giza.
244.4 / 195.85 x 1618 = 2.019
244.4 x 1.618 / 2 = 197.7196
So the ratio between the end height and the breadth is close to 2 / phi
For the "195.8, seems inexplicable", I had a go with my calculator at trying to find a connection with phi, or with anything for that matter, that could explain the curious value of the breadth of the great central chamber.
After a good half hour or so, I was delighted (and relieved) to find that yes, there was a Phi connection then with this curious number.
3,168 / 1.618 = 195.797
This is practically 195.8.
What's the significance of 3168?
3168 and 316.8 are values used in various units in several ancient sacred spaces, such as Silbury Hill, Avebury, Glastonbury and Stonehenge. The Station Stone rectangle there is 3168 inches long. And in fact the perimeter of the Great Pyramid is 3,168 Roman feet, and each base side is 3168 Roman palms. 1:3168 was a scale used in map making for a long time.
The number 316.8 is connected to the Astronomical Megalithic Yard:
1 AMY = 2.71542857 feet = 6/7 of 3.168 feet.
19.008 is 6 x 3.168 and 1 AMY is 19.008/7 feet so it follows that 1 AMY is 6 X 3.168 / 7 feet, or 3.168 x 6/7 feet.
And, since 3.168 = 176 x 18 / 1,000, then 1 AMY = 176 x 18 x 6/7,000 feet
Robin Heath, in The Lost Science of Measuring the Earth, mentions this 3168 number. At Stonehenge, each pair of Aubrey holes is separated by 31.68 feet. One AMY is 2.71542857 feet and Robin Heath writes: '2.71542857 feet is 6/7 of 3.168 feet, demonstrating the AMY’s connection with sacred geometry.’
The fraction 176/175 (or 22/7 x 8/25) is significant, as noted in John Michell and Robin Heath's book, The Lost Science of Measuring the Earth, page 13. This is the link between certain units of measurement to make up for errors in pi derived lengths. 175/176 is used as a link between long and short version of Greek foot, eg 1.008 to 1.01376. Also, the embankment circle at Stonehenge is 1056 feet in circumference, and 1,056 / 6 = 176.
And 1.76 x 180 = 316.8.
The Third Pyramid
The dimensions of the third pyramid are as follows. (Again, the quotations below are from Flinders Petrie's The Pyramids and Temples of Giza)
(...)
What, then, is to be reckoned as the size of the true base of the Pyramid? Not the present edges of the granite, for they are utterly rough. And not the ends of the fine-dressed edges of the joints, for they end at various levels. But looking to the fact that all the courses of granite are intended to be equal, and a rather short two cubits each, it seems most suitable to take a mean of all the granite courses (since the upper are not thinner than the lower ones),and reckon the intended base of the Pyramid at one mean course height (40.3 ± 1.5) below the first joint. Remembering also that the Second Pyramid courses average two cubits each near the base, and the bottom course was just two cubits above the pavement.
At this level, then, the various data of the intended surfaces give the following size for the base, reducing those data that are on higher levels by the angle 51º 0' :—
Length. Difference Angle. Difference
from Mean. from Mean.
N. ... ... ... ...
E. 4149.2 – 4.4 + 16' 48" + 2 45"
S. 4157.8 + 4.2 +12' 23" – 1' 40"
W. 4153.9 +.3 + 12' 57" – 1' 06"
Mean 4153.6 3.0 + 14' 3" 1' 50"
The N. end of the W. side could not be reached, after several attempts; and hence the lack of knowing the length of the N. or azimuth of the W. side."
"Considering the various sources of error : that the dressed granite in situ. is very irregular; that the 1st course joint at S.S.W. may easily be estimated too far out; and that we have no guarantee in the moved granite blocks, or the limestone from the upper part, that the courses were horizontal (on the contrary, one granite block has two different joint surfaces, 1º 40' different); the best conclusion seems to be 51º 0' ± 10'. But from a consideration of the granite courses (see below), the angle would be 51º 10' 30" ± 1' 20"; and this might well be adopted, as being close to the very uncertain result from the measured angles.
Hence the height of the Pyramid would have been 2564 ± 15; or 2580.8 ± 2.0 by the granite courses.
(...)
it is worth notice that the granite just covered one quarter of the height of the Pyramid, the total height being 4 x 641 ± 4 Conversely this may be taken as giving a determination of the original total height, perhaps more accurately than by the varying angles of the Casing, thus :— 645.2 (± .5 (?) for uncertainty of paving) x 4 = 2580.8 ± 2. And this yields an angle of 51º 10' 30" ± 1' 20".
In metres, the base becomes 105.50144 m ± 0.0762 and the height 65.1256 m ± 0.381 or 65.55232 m ± 0.0508.
The base divided by the height gives a figure close to Phi: 4,153.9 / 2,564 = 1.62
If we use the maximum height allowed by Flinders Petrie's error margin, ± 15, Phi is arrived at more closely still:
4,153.9 / 2,564.15 = 1.61999
So in the third pyramid, something close to Phi is arrived at by dividing base by height, whereas in the Great Pyramid, Phi was arrived at by dividing the slant height by half the base.
Martin Doutré and Phi feet
For researcher Martin Doutré, a Phi foot is made up of Phi inches, each worth 1.61803 inches.
The perimeter length around the base of the Great Pyramid was designed to represent 1/2 of a minute of arc for the ring of the Earth. Inasmuch as 3 separate and slightly different geodetic systems were in common usage, the Priest/ mathematicians assigned marginally different perimeter codes to the Pyramid when working in either the PHI based or "11" series geodetic, "ring of the Earth" systems. Similarly, the vertical height was exactly 453.049492 feet (280 PHI feet or 168 Megalithic Yards)
Martin Doutré points out that the height of the Great Pyramid is 280 x Phi feet.
The Layout of the Pyramids at Giza

I quoted Flinders Petrie on the positions of the pyramids earlier, here it is again:
The relative positions of the three larger Pyramids to one another were completely fixed in the triangulation, which included them all. The following are their distances apart, as measured on parallels inclined – 5' to true N.— i.e., at the mean azimuth of the First and Second Pyramids; and also the distances, and the angles from these parallels, of the direct lines from one Pyramid to another:—
N E Direct
Centre of First to centre of Second Pyramid 13931.6 and 13165.8 = 19168.4 at 43º 22' 52" Centre of First to centre of Third Pyramid 29102.0 and 22616.0 = 36857.7 at 37º 51' 6" Centre of Second to centre of Third Pyramid 15170.4 and 9450.2 = 17873.2 at 34º 10' 11"
There does not appear to be any exact relation between their centres, or between the corners; and from the nature and appearance of the ground, and the irregularity of the peribolus walls, it would not seem likely that any connection had been planned.
(Italics my own)
There is a site plan - possibly the most famous site plan of any ancient monument, thanks to Robert Bauval. He was the first to make the connection between the three largest pyramids at Giza and the stars that make up the belt of Orion.
And what's more, Phi does not limit itself to the inside and outside of the Great Pyramid - it's also in in its relationship with the other pyramids at Giza.
There's an article on this called 'Golden ratios in Great Pyramid of Giza site topography' by Gary Meisner on https://www.goldennumber.net/great-pyramid-giza-complex-golden-ratio/, which shows Phi ratios in three small pyramids next to the Great Pyramid, in "the placement and dimension of the middle pyramid in relation to the perimeters of the two outside pyramids", the distance between the corner points of the bases of the Pyramids of Queens, the relative positions of the two largest pyramids of the complex, and in the topography of the smaller pyramid in relation to the middle pyramid. Other researchers quoted in this article (Chris Tedder, Jiri Mruzek) have also made some very interesting finds, which Gary Meisner has incorporated into a diagram.
The diagram below is from Glen Dash...

On the basis of the above diagrams, Meisner created the diagram below:
This analysis shows a very close alignment of the pyramids to these golden ratios:
The golden rectangle formed by the apex points of Khafre and Menakure [sic] has sides with a ratio of 1.613.The golden rectangle formed by the apex points of Khufu and Menakure[sic] has sides with a ratio of 1.618.The ratio of the base of Khufu to that of Khafre averages to a ratio of 1.610.
Gary Meisner
The Blue Rectangle
The value in metres of the western side of the blue rectangle is 354.3. The number was familiar to me. There are 354.36708 days in 12 lunar months.
If the western side of the blue rectangle on the diagram is supposed to encode the number of days in 12 lunar months, then the longer side, the one that runs West to East, is this figure times Phi. That would make the blue rectangle a sort of lunar golden rectangle, and so if you take the actual value of 12 lunar months in days as your measurement in metres, 354.35708 (rather than 354.3) and multiply it by 1.6180339887, you get an even better correspondence between both sides, in terms of phi. 354.36708 x 1.61803399= 573.3779799. 354.3 x 1.618 = 573.269442 and the longer side of the blue rectangle is 573.4, so it seems that the lunar figure fits very well.
The blue square is crucial to the site layout because it incorporates the relative positions of the centres of all three of the bigger pyramids.

The Red Rectangle
The dimensions of Gary Meisner's red rectangle (or Chris Tedder's blue one) , 239.5 m and 385.7 m are of also very interesting. It's worth making the point straight away that the blue rectangle and the red rectangle together are enough to mark out the positions of the apexes of the three larger pyramids on the Giza complex. Nothing else is needed.
Firstly, as Gary Meisner points out, 385.7 / 239.5 = 1.6104. This is very close to 1.618. But why is it so close but not exact? I took to playing around with my calculator for a while and I found that if you add 1.618 metres to the longer side of the red square, and then divide it by the value of the shorter side, you get a number much closer to Phi: 1.617194.
(385.7 + 1.618 ) / 239.5 = 1.61794
I also found that the square of each of these numbers, 239.5 m and 385.7, adds up to make 206,124.74.
This is similar to a number we have seen before: a cubit is normally defined as 20.61818 inches, there are 206.12 (or 206.14) miles between the Mont Saint Michel and Saint Michael's Mount, and the width of the King's Chamber was found to be 206.12 inches by Flinders Petrie, or 100 cubits of 20.612 inches.
Also, the number of days in a year divided by 20, squared and then divided by phi is 206.1213.
The number of days in a year divided by the number of days in 12 lunar months times 200 is 206.1419.
And 10 / 6 x 200 / 1.618 = 206.01566
The diagonal in metres of this red square, i.e. the distance between the centres of the second and third pyramids is the square root of 206,124.74, which is 454.0096.
This is almost exactly the same value Flinders Petrie gives: 17,873.2 inches, or 453.97928 metres.
The distance in miles between Skellig Michael and the Mont Saint-Michel is 454.96 miles, which is very close to being 206.14, the value in miles between the Mont Saint-Michel and Saint Michael's Mount, squared and divided by 100, plus the value in days of a lunar month, 29.53059, which makes 454.4676.
So, as we've just seen, the number 454 can be arrived at by multiplying 206.12 by 1,000 and the taking the square root of that, and the number 454.4676 is linked to the number 206.14 in this way: (206.14² / 100) + 29.53059. Also (206.12² / 100) + 29.53059 = 454.385134.
The short side of the red rectangle, adjacent to the blue, is linked to the longer side of the blue in this way: 573.4 / 239.5 = 2.39415. If the short side of the red were taken to be a little shorter at 239.45, then we would get 573.4 / 239.45 = 2.39465, which means that the square of 239.45 is 57,340.
√(573.4 x 100) = 239.4577
This means that the shorter side of the red is very close to being the square root of 100 times the long side of the blue square.
The Yellow Rectangle
There's another solar / lunar figure too, the length of one side of the middle pyramid, 215.3 m, plus the distance to the extended southern side of the Great Pyramid, 131.3m, makes 346.6m. There are 346.62 days in an eclipse year, or draconic year, the time taken for the Sun (as seen from the Earth) to complete one revolution with respect to the same lunar node.
The yellow rectangle has one side of 346.6 metres.
The yellow rectangle defines the position of the two larger pyramids with respect to each other.
On the Glen Dash diagram the side of the second pyramid works out at 215.2 / 215.3 metres, and Flinders Petrie gives a mean dimension of 8474.9 inches, which works out at 215.26246 m.
I tried multiplying the value of the base side of the second pyramid by Phi.
215.26246 x 1.618 = 348.29417
The distance between the centre of the third pyramid and the eastern side of the second pyramid, 347.66631 m, is close to being in golden ratio with the base side of the second pyramid.
If you take a rectangle with a short side made up by the base side of the second pyramid and the long side the distance between the western side of the second pyramid and the western side of the Great Pyramid, then you have an almost golden rectangle with a ratio of 1.61508.
The base side of the Great Pyramid is worth very close to 2/5 of the east-west line between the centres of the first and third pyramids, as 577.4 x 2 / 5 = 230.96. And 346.6 / 2 x 3 = 519.9, and this closely matches another measurement: the south side of the Great Pyramid to the south side of the second. 520 / 3 x 2 = 346.667, which is the eclipse year in days.
Centre to centre, the north-south line between the two bigger pyramids is, in metres, the value in days of 12 lunar months, and southern side to southern side, the North-south line between the two bigger pyramids is the value in days of an eclipse year, converted to metres. Obviously, the link with Orion is famous, but I was surprised to find the importance of these lunar and solar figures here. Together the value in days of the eclipse year and twelve lunar months combine to give, in metres, the distance between and the relative sizes of the Great and second pyramids.
The Glen Dash diagram is not "inclined to 5' to true N.— i.e., at the mean azimuth of the First and Second Pyramids" (Flinders Petrie) but only allows for north - south or east - west dimensions, and with only one decimal point. This would explain the inaccuracies I was getting when trying to calculate distances according to coordinates from that diagram, one figure for the distance between the eastern sides of two pyramids and a slightly different one for the western sides, for example. Flinders Petrie's figures do take into account this 5' to true North however.
A purple golden rectangle
There are two other lengths that are in a phi ratio that I stumbled across, and both run along an east to west direction: the first is the width of the whole site, from the western side of the third pyramid to the eastern side of Great Pyramid: 741m. The second is from the centre of the third pyramid to the Western side of Great Pyramid: 458m.
741 / 458 = 1.6179
As it happens, the long black line on the diagram which makes up the width of the site (western side of third pyramid to eastern side of the Great Pyramid) is exactly the same length. This means that we have another golden rectangle, drawn in purple on the diagram.
The black line, of the width of the site, 741 m can be linked to the solar year like this: 365.242199 x 2 - (365.242199 - 354.62) = 741.126597
365.242199 is the number of days in a year. 354.62 is the number of days in 12 lunations.
I looked for an instance of the solar year on the site, something that might be 365.24 metres. The best I could find was this. The distance between the north side of the Great Pyramid and the north side of the second pyramid is 361.6 m. Curiously, 365.242199 - 3.618 = 361.624199. So the distance of 361.6 m seems to represent the number of days in a year minus 3.618, the number that comes up again and again in ancient sacred structures.
The green line is in phi ratio with the distance between the west side of the second pyramid and the west side of the Great Pyramid.
The distance between the north side of the Great Pyramid and the south side of the third pyramid is 907.8 m.
346.62 x 2.618 = 907.45116
It's difficult to be sure of the measurements on the Glen Dash plan, if you try and take the distance between two points, they don't then tally with other distances when they should. I decided to start the whole thing again but with the Flinders Petrie figures, which are much more precise, and take into account the orientation of the site, just of true north, plus the triangulation points were spread out all around the site, whereas on the Glen Dash plan, all measurements are related to the centre of the Great Pyramid. You can see on my diagram that the short side of the blue square and the long side of the red square should add up to exactly the long side of the purple square, and they don't. This is a bit frustrating, so I decided to go back to Flinders Petrie's figures. I plotted his measurements in the diagram below, worked out the others from those, and then simplified them into another diagram, see below.


The side of the red rectangle which measures 240.03508 m may reflect the number of hours in a day. The long side of the red rectangle is very close in metres (385.328162) to the number of days in 13 lunar months (383.89767). The whole rectangle formed by the arrangement of the three pyramids is very close to a 9:11 rectangle, or to be exact, a 9:10.9972 one. The perimeter of the rectangle defined by the corners of the Great Pyramid and the third pyramid, with sides of 742.370875 m and 907.11527 m, is one metre short of 3,300 m.
The ratios above are more approximate than exactly Phi.
Phi, or something close to it, or something close to it, comes up again and again, I'm not sure how anyone can say it's a coincidence.
In any case, I think that at this stage it is inconceivable that phi and pi being present at Giza may be some sort of fluke, that the people who designed and built the Great Pyramid, the other pyramids and the temples there didn't know about 3.1416 or 1.618. In fact I think that phi in particular is the key to the Giza Pyramids, a golden key.
Often, the reason given by people don't believe the ancient Egyptians could not possibly have known about phi is that there is no written record of it, from dynastic or pre-dynastic times.
Archeologists and egyptologists haven't found any written record of it, therefore the pyramid builders couldn't possibly have known about it. But first of all, how can we know what the ancient Egyptians called phi, how they referred to it? It might have been Atum for all we know. Or Ptah...
And secondly, the absence of proof does not prove the Egyptians didn't know about the golden ratio.
In any case, how can we possibly know for sure what was known five thousand years ago, based only on surviving texts? Why not read the evidence in the stones?

The Archeologist of the Future
Five thousand years have fled, let us suppose.
And lo, and archeologist appears,
Searching for records of our joys and fears.
And haply out of all our verse and prose
One book alone remains. How it will pose
His plodding brain, after that flight of years,
To come on Alice swimming in her tears,
Or Father William, an eel upon his nose!
He'll stare and gasp at Tweedle-dee and -dum
And gape at incancescentwords that mock
Invention, Bandersnatch and Jabberwock,
And, fancying angry eggs and talking flowers,
No doubt will think his fifth millennium
A far less entertaining time than ours.
Leonard Bacon
in What Cheer, An Anthology of American and British humorous and witty verse gathered, sifted, and salted, with an introduction by David McCord, Coward-McCann inc New York, 1945
The sun and moon cycles inscribed in the pyramid layout at Giza
Phi can be found at Giza in conjunction with numbers connected to lunar and solar cycles, inscribed in the pyramid layout in metres.
The blue rectangle combines the number of days in 12 lunar months and phi.
The yellow square contains in metres the number of days in an eclipse or draconic year.
The purple rectangle combines phi with the number 741, linked to the solar year and 12 lunations like this: 365.242199 x 2 - (365.242199 - 354.62) = 741.126597
365.242199 is the number of days in a year. 354.62 is the number of days in 12 lunations.
These rectangles and this square actually define the space at the Giza complex, they are not just random. The blue rectangle alone goes through the apexes of all the first two pyramids and the meridian of the third pyramid's apex. The red rectangle fixes the position of the second pyramid in relation to the other two, as it passes through the third pyramid and runs along the side of the blue rectangle which fixes the centres of the Great Pyramid and the third pyramid.
The yellow square fixes the size of the Great Pyramid and second pyramid, as it goes through the south western corner of each of them, so in relation to the blue rectangle, which fixes the centres of these two pyramids, it settles how far they should extend. These pyramids all having perfectly square bases, the other three corners are also then provided for by the yellow square. The purple rectangle then confirms the size of the Great Pyramid in relation to the centre given to it by the corner of the blue rectangle, as it runs along its western side. It also confirms the position of the third pyramid, as the south west corner of the rectangle goes through its centre. The short side of the purple rectangle is also in phi ratio with the distance between the western side of the third pyramid and the eastern side of the Great Pyramid, thus defining the width of the site and the lengths of the Great and third pyramids, in conjunction with the other rectangles.
All of this seems to fit into the site layout according to Orion's belt, as well as the size of the Great Pyramid being representative of our planet.
To accept that this was intentional, you'd need to be open to the idea of the builders of the pyramids having used the metre.
Is there any other hint of the metre having been used at Giza? If you take the Great Pyramid's base in metres, double it and subtract the value of the height in metres, you get: 230.363 x 2 - 146.71 = 314.016
That's close to pi times 100. I didn't work that out myself, this is from this website: http://metricviews.org.uk/2013/06/was-the-metre-invented-by-the-ancient-egyptians-4500-years-ago/
I won't go into the question of the metre at Giza now, this post is already very long. I will look at it in another post.
Atum
Why might we find Phi at Giza?
Again, John Anthony West gives us a clue, invoking the god Atum:

Memphis revealed the work of Ptah, producer and animator of form. Ptah is Atum, fallen to earth. He is the coagulating fire, simultaneously cause (of the created world) and effect (of the scission). Ptah is phi, the creative power immanent in Atum but locked in Atum in his fall to earth. Ptah is not free. He is bound by Set, principle of contraction. That is why he is always pictured bound in swaddling clothes, with only head, hands and feet free. And Ptah is also the prototype of the Greek Hephaistus (...), the smith in his subterranean laboratory (...)
The Serpent in the Sky, p. 127
Phi is a creative power for the Ancient Egyptians. On the following page, John Anthony West explains that "Ptah is the personification of the creative aspect of Atum." Atum was created by Tum, transcendent cause, out of the primeval waters of Nun. The name Atum may be derived from the verb tm which means 'to complete' or 'to finish. Atum is a creator god, he is the substance of everything in the world. Atum is the first God, he has created himself from the primordial waters (Nu), sitting on a mound (a benben), perhaps he even is that mound.
You can start drawing up Egyptian inspired interpretations of the significance of the Michael mounts in North-West Europe: rocky islands can be construed as Atum, his manifestation, drawn up from the primordial waters, which are represented by the sea. You could begin to think that any rocky island or mound might represent Atum, here on Earth, but that those linked to phi are somehow even more special. Skellig Michael, Saint Michael's Mount and the Mont Saint-Michel are all linked to the direction of sunrise on days when light and darkness are in phi ratio.
In fact, although Atum is also a solar deity, he is in fact more closely linked to the midday sun and to sunset, and Ra is the deity associated with sunrise. Sunrise is also linked to another solar deity, a ram-headed scarab named Khepri. He is the young sun god, whose name is derived from the Egyptian hpr "to come into existence".

In the Book of the Dead, the sun god Atum is said to ascend from the chaos-waters, looking like a snake, renewing itself every morning and slithering across the surface of the sea.
Sometimes Atum is shown as a serpent, the form he returns to at the end of the creative cycle, but mostly he is shown as a man wearing either the royal head-cloth or the dual white and red crown of Upper Egypt and Lower Egypt.
The most important reason for considering it special is that phi is inbuilt in life. Many proportions reveal a ratio close to Phi, the way branches grow on trees, the way seeds form in flowers, the way human bodies and faces are structured. In fact, many life forms contain phi, and that there is an almost unlimited number of examples to chose from to illustrate phi in nature, starting with what we see in the mirror, and the trees outside the window. Once you understand that this irrational number called phi is central to life, then you begin to think of it as creation itself.
Le Nombre d'Or ne joue pas seulement comme fonction d'une proportion ideale, mais sert de base a une philosophie faisant la relation entre l'etat metaphysique et a l'etat physique. C'est en cela que consiste son charactere sacre.
The Golden Number doesn't only play the function of ideal proportion, but it serves as the basis of a philosophy which links metaphysical and physical states. That is the way in which it is sacred. (My translation)
R.A. Schwaller de Lubicz, Le Temple dans l'Homme, quoted in The Sphinx and the Megaliths, by John Ivimy, 1974. (Great book I picked up in Hay)
This brings the number Phi into the realm of metaphysics. When John Anthony West and Schwaller de Lubicz suggest that phi is not actually a number but a function, are they simply alluding to the usefulness of a fraction closely related to phi in value, and used in geometry, and measured in nature? Or are they suggesting that this ratio is in fact a central part of whatever it is that links the physical world with the non-physical world, a central part of life, and death, and creation? You might want to distinguish between phi as an irrational number, and applied phi, the way we know it best, in nature, in geometry, in Fibonacci sequences. Is phi, as an irrational number, really a number, that is, what is its ontological status?
On the one hand, phi, as applied phi, is immensely practical and observable, it is immanent to this world. Does this immanence channel anything of the divine? Can Phi, as irrational number, be the expression, or even the essence of the divine?
In recent centuries, number has not been a part of philosophy. Over the last few decades, debates have centred on the nature of consciousness, on post-modernism, on deconstruction, on feminism, on identity, and various ethical questions. Number is not even a contender for most philosophers' attention, and even recent works on ancient philosophers often completely overlook the mathematical side of things, presumably on the basis that ancient maths have been superseded by contemporary maths, and are in no way useful, and so in no way interesting. The same is true of ancient medical writing, by the pen of very well-respected Muslim philosophers such as Avicenna, and work on alchemy, researched by respected thinkers such as Newton - those bits are ignored because they don't fit with a contemporary understanding of the world.
The point seemingly made by Schwaller de Lubicz is that certain numbers (or functions) such as phi actually can define metaphysical questions. When you read works by Plato or Aristotle, you can choose to just focus on the ethical or political questions, as is often the case, and stick to the sections on the ideal state, or the nature of the soul. Alternatively, you can also read the parts that insert themselves less easily into the contemporary way of thinking you can try and see them as genuine idiosyncratic attempts to understand the entire fabric of the world. When I was a philosophy student, Plato was presented as the original and the best philosopher, which may well be true. However, Plato's accounts of what things were made of, his concepts of idea, of ideal, of form were never considered seriously as capable of explaining the universe and its structure, more as curiosities, presented as fascinating little snipets into the minds of long superseded civilisations. I don't pretend that they can be - I don't know. I make the point only to show the contrast between the reverence still shown to Plato and the unspoken dubiousness towards some of his most central tenets, implicit in much of the contemporary presentation of Plato. ( And I won't begin the mention the single most popular thing Plato is read for today, Atlantis - the dubiousness shown by most people towards the subject is well-known, though I'm not sure why as it's clear large parts of the world have been submerged in recent millennia)
Today, we afford the Ancient Greeks the honour of having been the first to think philosophically, partly on the basis that they had a language capable of producing concepts. And perhaps partly n the basis that we actually understand their language have heard a very well respected thinker say that, in contrast to the Greeks, the Egyptians were not capable of philosophy, purely because of the limitations of their language.
Over the last thousand years or so, the great minds of Ancient Greece have not only been respected and well studied, but they have been absolutely crucial to the development of European culture. Not so with Ancient Egypt, from which we seem only to have inherited certain religious ideas, and only in a covert way, generally unacknowledged except in YouTube videos. Isis may be connected to the Virgin Mary, Horus to Jesus, various symbols of Egypt may have been incorporated into the Christian Church, and then, there is the concept of monotheism - the earliest known instance of a one god religion was the short lived cult of the sun god Ra.
In the Serpent in the Sky, John Anthony West shows how difficult it is to actually understand all the nuances of the old Egyptian language, and how today's readers of the old texts are unfortunately stuck in many cases with nonsense, despite the translators' best attempts.
So, the Egyptians certainly did not know about phi and pi? Despite the many limitations we face when trying to understand and really make sense of the ancient texts, the untranslatable words, the slippery nature of meaningfulness, we are sure they had no concept of phi and pi - really?
Pi and Phi may be just quite nice numbers to us, but they may be sacred concepts to another. They may have terms and symbols attached to them that we already know, but attach a different meaning to.
Though number is central to our culture today, it is no longer central to metaphysics.
Number, star-gazing, and the interplay of what we can and cannot see, have shifted from the domain of philosophy over to the sciences. The creative energies of our time are focused to a large degree, on developing Einstein's legacy, and creating wonderful concepts that owe something to children's and sci-fi literature, and to the counter culture of the seventies.
The Sun and Phi
So are Phi and Atum / Ra / Ptah interchangeable? Is the golden ratio the captain of the sun's ship? It's not just life and creation that are bound to Phi, but the sun as well.
What is it about solar power or solar cycles that connects it to the strange powers of 1.61803...
Curiously,
Solar year / 12 lunations x 200 x φ = (solar year / 19.99901)² ≈ (1 lunation / φ)²
(Solar year = 365.242199 days, 1 lunation = 29.53059 days)


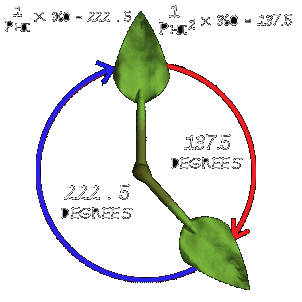






Comments