70. Inch and Metre: a Match Made in Giza
- M Campbell
- Mar 12, 2024
- 16 min read
Updated: Jul 21, 2025
Below is a table showing the dimensions of the sides of the three main pyramids, and of the Great Giza Rectangle which links the north west corner of the Great Pyramid and the south-east corner of the third pyramid - just the dimensions of five key linear lengths, to keep it simple. From this, what can we learn about the presence of the inch and the metre at Giza? We can use the modern value for the metre, which is 2.54 cm to the inch, or we can also consider using a "metre" of 29.53059 x 4/3 inches. Do metre and inch co-exist harmoniously at Giza?

The table
In the first column, in red, the table shows what I have called the astronomical and geometric value. By this I mean a value that is derived from the square root of three, from pi, and from either simple integers such as 2, 3, 4, 5, 8, and 10, and from numbers of days in astronomical cycles, such as 29.53059 days in a lunation, 223, the number of lunations in a so-called Saros, or Chaldean period, 235, the number of lunations in a Metonic period, and 254, the number of sidereal months in a Metonic period. The second column, in orange, shows the astronomical and geometric values in modern metres, for these five lengths. The equations which led to these values are to the right of the table, in blue for the values in inches, and in dark green for the values in metres.
2. The Great Pyramid side
Looking at the equations for the values in inches first, we have 5000 π / √3 for the side of the Great Pyramid. This gives an astronomical / geometric value of 9068.9968 inches, if we use the values for the irrational numbers from a calculator. What is the significance of this? Well, on a geometric level, we have pi and √3, so the circle and the triangle are referred to. These are simple, symbolic shapes which may convey something about the universe, about consciousness, and how they are understood by human minds. The irrational numbers, being beyond the scope of human definition may symbolise the divine (there is no number we can define exactly, which, squared, makes 2 exactly, or 3, or 5).
Also, these irrationals represent a system of measure and integration of many cycles of time. The presence of π / √3 indicates the representation, through geometry, of this precise system of time measure.
civil year x draconic year / (lunar year x lunation) x 3 / 20 ≈ π /√3
number of lunations per year ≈ π /√3 x 300 / 44
And to a lesser extent, sidereal month x 3/2 x 1 000 000 / (25 920 x 29.53059²) ≈ π /√3

It may also be that the 33 year cycle of the sun and moon is linked to 2π /(3 x √3), as there are 12 052.9926 days in 33 years, and 20 000π /(3 x √3) = 12 091.9958, a difference of 39 days. The astronomical and geometric value for the side of the Great Pyramid is 9068.9968 inches, which is 230.3525 m. The equation for the value for the side of the Great Pyramid in metres is 5000 π / √3 x 254 / 10 000. This is unsurprising because 2.54 cm make an inch. However, it is worth highlighting the importance of the number 254: it is the number of sidereal months in a Metonic period. Even if the metre hadn't become a modern unit, in the aftermath of the French revolution, we would still find it here at Giza, because the numbers that matter are connected to astronomical cycles, so 19, 235, 254, 223, 60, etc. When we convert the equation for inches to the equation for metres, we aren't just using any old at coefficient, we are using a highly significant time number, in which the sidereal and synodic months reconcile almost perfectly with a certain number of solar years, which happens to be 19.
The values arrived at through these equations, both the inch and the metre, fall slightly short of the values given by Flinders Petrie. This is consistent throughout the site, in fact. It could be a due to slight differences in the inch, or in the values for the irrational numbers, or in the values for the cycles of time in days, or all three. But overall, multiplying these astornomical and geometric values by 1.0002766, (or even 1.0001415) works well to bring the values in line with Flinders Petrie's. Here I am using 1.00002766, referred to as "C" in the table above.
We obtain from these astronomical and geometric values 9 068.9968 x 1.0002766 = 9 071.5053 inches (or alternatively with the 1.0001415 coefficient 9070.2801 inches), and 230.3525 x 1.0002766 = 230.4162 (or, alternatively 230.3851 with the coefficient 1.0001415). By comparison, the value given by Flinders Petrie for the mean side of the Great Pyramid is 9068.8 inches.
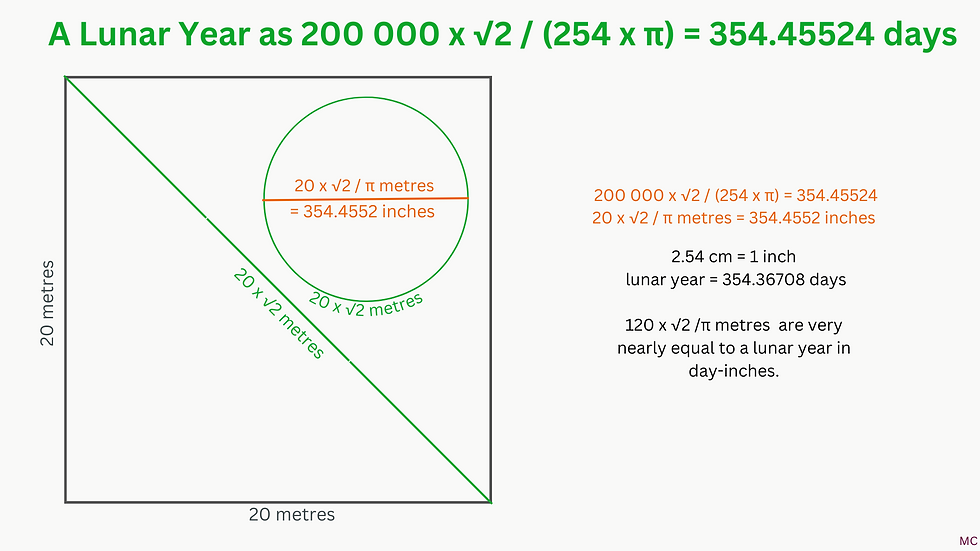
The square root of 2 can also link inch and metre to the moon, as 20 x √2 /π metres are very nearly equal to a lunar year in day-inches.
3. The second pyramid side
If we look at the astronomical and geometric values for the side of the second pyramid, we have 8471.2426 inches and 215.1696 metres. The equations from which these values are derived are 500 π / (√3 x 3) x 223 / 235 and 5 π / (√3 x 3) x 223 / 235 x 29.53059 x 254 / 100 respectively. Again, it is no surprise that we use 254 to convert from inches to metres, but this becomes very interesting in the context of the equation to give the value in inches in the first place, as the number of lunations in a Metonic cycle (235) and in a Saros cycles (223) are clearly referenced. So we have the system as a whole represented by π / √3, and then these very important numbers of months, synodic and sidereal, all together in one equation. The values then obtained by multiplying by C are close to Flinders Petrie's. We obtain 8471.2426 x 1.0002766 = 8473.5857 for the inches, and 215.1696 x 1.0002766 = 216.2294 for the metres. By comparison Flinders Petrie's value is a mean of 8474.9 inches.
4. The third pyramid side
If we turn now to the smallest of the three, the third pyramid, the astronomical and geometric value in the table is given as 4151.5332 inches, and 105.4489 metres. The equations from which these values are derived are 2000 π / (√3 x 3) x 29.53059² / 254 and 2π / (√3 x 30) x 29.53059² respectively. When we convert to metres, and thereby multiply by 254, we actually simplify the equation because there is already a 254 in the denominator for the equation in inches. If we then multiply these values by the coefficient C, we obtain 4152.6815 inches, and 105.4781 metres. Flinders Petrie's measure for the side of the Third Pyramid is 4,153.6 inches.
5. The Great Giza Rectangle: length and width
Now turning to the Great Giza Rectangle, which encompasses the north-east corner of the Great Pyramid, and the south-west corner of the third pyramid, we obtain astronomical and geometric values of 35 704.71189 inches and 906.8997 metres for the length, and 29 222.8685 inches and 742.1848 metres for the width. If the length in metres looks familiar, 906.8997, well spotted. The equations are as follows: length in inches: 5 000 π / √3 x 1 000 / 254. Length in metres: 500 π / √3. Once again, converting to metres actually simplifies the equation, removing the 254 from the denominator in the first equation that produces inches. And when we look at this equation for the value in metres, we can see the link to the equation for the side of the Great Pyramid in inches, as they are almost identical, but for a factor of 10. The Great Pyramid side in inches, astronomical and geometric value, is 5000 π / √3. The width of the site results from the equation 32 / 3 x π x 29.53059² for the inches, and 8 π x 29.53059 for the metres, if we use the value of 29.53059 x 4/3 inches for the metre, rather than 10 000 / 254 inches, or 80 000 π x 29.53059 / 254 inches if we continue to convert in the conventional way with 2.54 cm to the inch. Again we can see here that the equation to obtain the value in metres is simpler. Multiplied by the coefficient C, the values become 35 704.71189 x 1.0002766 = 35 714.5878 inches for the length, which is 906.8997 x 1.0002766 = 907.1505 metres. And for the width, we get 29 222.8685 x 1.0002766 = 29 230.9515 inches, or with the other coefficient 29 222.8685 x 1.0001415 = 29 227.0035 inches, and 236.2447 x 1.0002766 = 236.3100 metres for the width (or 236.2447 x 1.0001415 = 741.9989 metres). Flinders Petrie gives 35 713.2 inches for the length and 29 227.2 inches for the width.
Of course, the interpretation of the values of these five lengths at Giza is just one of many possible interpretations. However, the proportions between the five lengths do seem to back up the theory that they represent lunar and solar cycle ratios, as the diagrams below show.






6. The status of the metre at Giza
If these equations are correct, this implies that the metre, of 10 000 / 254 inches, has an integral place at Giza. It is part of the design, by virtue of relating to the inch via a key lunar number, 254. The value for the side of the Great Pyramid in inches corresponds to the length of the Great Giza Rectangle in metres, multiplied by 10. In other words, while a metre is 10 000 / 254 inches, the conversion between the side of the Great Pyramid and the length of the Great Giza Rectangle is 1 000 / 254. This is an indication that we should take the number 254 at Giza seriously.
We've looked at the values for these five particular lengths at Giza, the mean lengths of the three largest pyramids and the length and width of the Great Giza Rectangle, as products of equations which feature numbers derived from astronomy and geometry, notably π , √3, 29.53059, 223, 235, 254, as well as simple integers like 3, 4, etc. But if we look at the values of some of these lengths we can actually determine that they represent cycles of time. For example, the width of the rectangle in inches represents 80 solar years of 365.242199 years. 80 x 365.242199 = 29 219.37592. As a measure in inches it is just a little under the values obtained earlier, but only by a few inches. The astronomical value obtained earlier was 29 222.8685, so it is less than 4 inches under. The 80 years probably reference the 8 year cycle of Venus.
However, if we read the value in metres, using the astronomical and geometric value, 742.1848, this corresponds closely to the number of lunations in a 60 year period. 365.242199 x 60 / 29.53059 = 742.0960. If instead of the modern conversion ratio we use a "metre" of 29.53059 x 4/3 inches, then we get a closer match here. 365.242199 x 60 / 29.53059x 29.53059 x 4/3 = 29 219.37592. In fact, the reason this works well here is down to the interplay between the two periods, 80 and 60 years, which give rise to the 4/3 ratio.
My own interpretation is that the lengths at Giza represent time, and that they can mostly be read in inches, but can also be read in metres, and other units such as the Egyptian royal cubit. However, there is no one length at Giza which represents the Metonic cycle, or the Saros cycle. Instead, these five key dimensions that we are looking at here, as well as many other parts of the site, all seem to be parts of a puzzle, parts of a whole which must be understood as a system. There is no single unit with which to measure the site, as other units reveal different layers of meaning.
One thing we don't find with these measures at Giza is metres or inches present in integer numbers. For example, 5 metres, or 20 inches. That's not to say the architects never used integer values, just that I haven't found an example of this yet. At Giza, what we tend to find is numbers derived from astronomy and geometry expressed in inches and metres, as well as cubits, Saxon feet, Assyrian / Persian feet, Roman feet and Greek feet.
The day inch is well documented in megalithic sites in Brittany, see for example Robin Heath and Richard Heath's work. And there are instances at Giza where we can interpret a distance directly as a length of time that is important to astronomy and a measure in inches. For example, if we take the slightly longer value for the side of the Great Pyramid, what Flinders Petrie terms the mean socket sides, of 9125.9, we could say this expresses the number of days in a 25 year cycle: 9125, and so with all 4 sides added together, we could interpret the height of the Great Pyramid as 100 years divided by √3, or 100 / √3 x 100 = 5773.50269.
The pyramid base is 9068.8 inches per mean side, and 36 275.2 inches for the perimeter, which is 921.39008 metres. Divided by 52, this is 17.71904. Multiplied by 10, this is close to the number of days in 6 lunar months. Divided by 6, this figure gives a lunar month of 29.5317333, which is very close to the modern estimate of 29.53059. If the perimeter of the Great Pyramid corresponds to 6/10 lunar months, in modern metres, then one side can be thought of as 29.53059 days, a lunation, multiplied by the number of 7 day weeks in a calendar year, 52, multiplied by 3/20, which equals 230.338602 metres, or 9068.448888 inches.
In the same way, we can interpret the width of the Great Giza Rectangle as 80 years, also expressed in inches. When we read the width as 29 227.2 inches, which is Flinders Petrie's measure, it might be tempting to conclude that the inch cannot have been an important unit at Giza, or we would be seeing 30 000 inches, or 28 000, or some nice round number. However, it seems that at Giza the inch is associated with time cycles, so is going to be found in multiples of 29.53059, or 365.242199, or even simply of π / √3, which represents a system of time cycles (in my view). And the metres here seem to express lunations, so the width of this rectangle is close to the number of lunations in a 60 year period. Broadly speaking, the inch seems more closely associated with the sun and the metre with the moon.
For some people, working with a metre at Giza just seems wrong, totally anachronistic. So there are other ways of thinking about it. For example, we could say that the width of the Great Giza Rectangle expresses the number of lunations in 60 years multiplied by 10 000 / 254, with the "254 " interpreted as a lunar number. Or we can think of a similar unit or 29.53059 x 4/3 inches which is in fact slightly longer, worth 39.37412 inches. But at the end of the day, 10 000 / 254 inches make a metre, it's simple. Also, 29.53059 x 4/3 inches make something very very close to a metre, and this may be due to the cycles of 60 and 80 years being counted out in lunations.
We can also add that 254 years are approximately 1,000 lunations. The relationship between these two cycles, 254 years and 1000 lunations, seems connected to the inch / metre ratio.
Phi squared is about 2.61803, and 2.61803 modern metres x 29.53059 x 12/10 make 365.2534037 inches. This suggests that Phi squared / 100 metres corresponds approximately to the ratio between a solar and a lunar year. Also, 10 solar years in inches are approximately 1 lunation x pi metres.
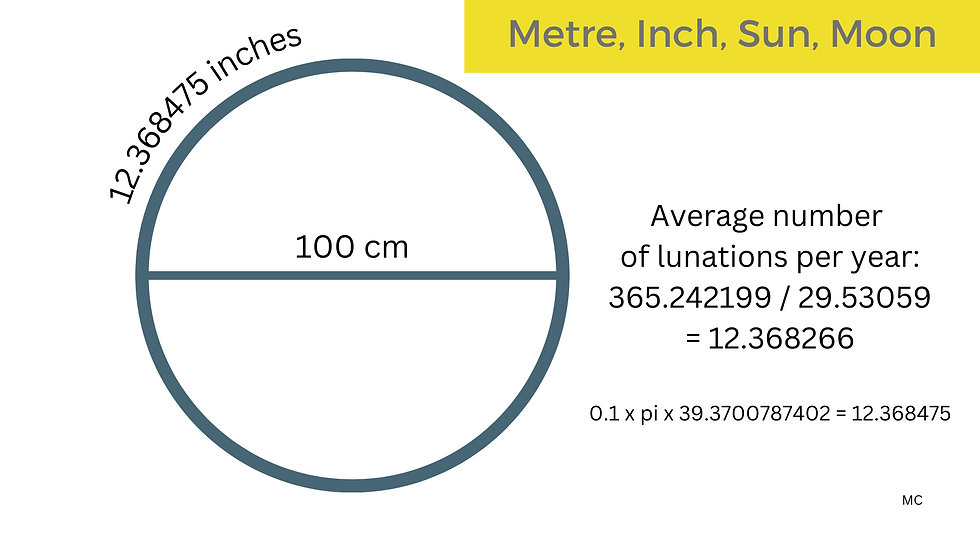
The metre allows lunar and solar links to be made when compared to the inch, for example a diameter of a circle of 100 cm has a circumference of 12.368475 inches, which is close to the average number of lunations in a year. And a circle with a diameter of 35.4326708 metres will have a circumference of 365.24836 inches.


We can ask ourselves why the number 254 was chosen to embody the ratio between inch and metre, seemingly quite inexplicably and suddenly in the early twentieth century. Yes, before that the ratio between inch and metre had been close to that, with various values for the metre expressed in inches in the region of 39.37 inches, or a little above that, up to around 37.3827 inches. In that time, comparative measurements varied, and the inch changed a little, and metric standards improved in quality, but when at last a final ratio was arrived at, the inch being re-defined in relation to the metre, it was with this ratio of 10 000 / 254.
7. A glance at the Giza plan, and the importance of 254
The table below shows interpretations of the dimensions in inches and in metres of so some of the most important features of the Giza site. Not only does the number 254 link the dimensions in inches and metres, but also the dimensions around the site, in inches and metres. Great Pyramid length value in inches is 10 times the Great Giza rectangle width value in metres, divided by 10: 9068.8 inches and 906.8562 m

A better correspondence can be obtained if the values derived from the irrational and lunar numbers are multiplied by around 1.0002.

The distances between the centres of the Great Pyramid and the second pyramid, and between the second pyramid and the third, relate to the Great Pyramid side as follows:
GP side x 3 000 000 x 254 / 22 = Great Pyramid - Second pyramid centre to centre
GP side x 58.2 / 29.53059 = Second Pyramid - Third Pyramid centre to centre.
The rectangles created by these two diagonals also display similar ratios, involving 29.53059.

By coincidence, the number 0.00254 is used as a coefficient, in a simplified representation of the Earth's oblateness, and used to approximate the variation in the length of a degree of latitude with latitude. 69.172 is the average length of a degree of latitude, in miles, and
0.00254 is the coefficient that modifies the length based on the latitude.
8. The Pyramid of the Louvre

We can also ask ourselves why M. Pei, the architect of the pyramid of the Louvre, chose to express the lunar and solar relationship between the inch and the metre in his creation. As Jim Wakefield has observed (1), the dimensions of the Louvre pyramid are 35.42 metres for the length of the base and 21.64 metres for the height (unfortunately no more precise figures are available). The 35.42 seems to reference the number of days in a lunar year, 354.36708, divided by 10, and the height of 21.64 metres is the diameter of a circle with a circumference of 223.0448 feet, perhaps a reference to the Saros cycle. The height in metres is twice the base side in feet: 21.64 metres are 354.3307 feet x 2 / 10. A circle with a diameter of 35.42 metres has a circumference of 365.076 feet.
Whether deliberately or not, the architect has made, in metres, the slope of the pyramid almost the same length as the side of the third pyramid in inches, divided by 100. √(21.64² + 35.42²) x 100 = 4148.88998. If the measure of the glass pyramid side is in fact 35.436708 metres, the result for the slope is 4152.1680. Petrie gives 4153.6 inches. Which means we could interpret the side of the third pyramid at Giza as √((354.36708 / 10 000 x 24 x 254)² + 35.436708²) x 10 = 4150.2 inches. It seems these ancient measures are still at play in today's world.
9. Looking for inches, metres and other units in multiples of astronomical numbers
It might be worth considering trying to interpret other ancient sites by looking at their dimensions as expressions of astronomical systems, and this could be done by reading the dimensions in inches, and also metres, and other units that work at Giza, in order to try to understand the design concept. At Stonehenge, for example, reading the dimensions in metres offers intriguing possibilities. The Sarsen circle diameter between the inner sides of the stones is according to Flinders Petrie 1167.9 inches, but taken as 1162.62 inches, just over a 5 inch difference, this could be interpreted as 29.53059 metres.

Also at Stonehenge, reading the dimensions of the station stone rectangle in metres allows us to see the role a 20 x 20 metre square could play in the design. Such a square gives rise to a spiral of Theodorus which fits perfectly onto the rectangle.



10. Al-kīmiyā
Before modern science was invented, one of the branches of natural philosophy that concerned itself with studying the natural world was alchemy. The word in fact comes from the Arabic, and gave rise to the word "chemistry". According to the Wallis Budge, the Arabic word al-kīmiyaʾ actually meant "the Egyptian [science]". Ridicule has been poured over the idea of searching for wonderful remedies, elixirs of everlasting life, philosophers stones, regarding the world as made from only four substances, and making gold from mercury. But there is an aspect of alchemy that is relevant to this analysis, and perhaps more generally today, which gives a framework within which to understand the world. In it, the sun and the moon are principal characters, and
Isis was the wife of Osiris and the mother of Horus. She was associated with the order of the cosmos, and with the moon. Osiris was also associated with the moon, killed at the full moon, and then resurrected. His body was broken up into 14 parts, a reference to the 28 days of a moon cycle. Osiris was also associated with the sun in that, the sun would pass through the Underworld at night, and that was Osiris's realm. Horus's eyes were associated with the sun and the moon.
Throughout the history of alchemy, at least what we know about it today, the imagery of a marriage between the sun and the moon, giving birth to a child, has endured. Perhaps what we see at Giza, with the inch mostly connected to solar periods and the metre connected to solar and lunar periods, is related to this idea. If we consider the Egyptian royal cubit as 365.242199 / 354.36708 x 20 = 20.613777 inches, or 0.5235899 metres, we see the twin powers of the moon and the sun uniting.
We know that the metre allows us to associate the Egyptian royal cubit with pi and Phi squared. 3.14159 - 2.61803 = 0.52356, fairly close value to 0.5235899. If we combine this with the formula which gives the value of 20.613777 inches to the cubit, we can say that:
(365.242199 / 354.36708 x 2 / 1000 x 254) + 2.61803 = 3.1416199, which is a pretty good approximation of pi. If we associate pi with circles, and cycles, and Phi with life, the Egyptian royal cubit as it is understood in English inches and metres, gives us a beautiful picture of life, as part of the cosmos.


Conclusion
Analysing the measures of the main three pyramids of of Giza, and the rectangle within which they sit, reveals numbers which are related to lunar and solar calendars, in particular to various ways of reconciling the cycles of the sun and the moon: the ratio between the solar and lunar years, the draconic year, the Metonic cycle, the 60 year Chaldean cycle, and the Saros cycle. It could be that the use of the inch, the metre, and also the royal Egyptian cubit, is designed to showcase these numbers.




Comments