In the last post, I explored the concept of squaring a circle, how it is linked to units such as the mile, in relation to the equatorial circumference, and its application in ancient sites such as Giza.

John Michell's squared circles

John Michell discovered a squaring of the circle at Stonehenge, in this case not by area but by circumference and perimeter. To begin with a circle is drawn with a diameter of 7 920 000 feet. This diameter represents the size of the earth, not in miles (which is a correct mean diameter with pi as 864 / 275, and the mean circumference as 24 883.2 miles) but in feet. The circle is inscribed within a square with sides of 7 920 feet, and a perimeter of 7 920 x 4 = 31 680 feet. The squaring of the circle consists in then drawing another circle which has the same circumference as the square. As pi is irrational, it is impossible to exactly match the perimeter of the new square to the perimeter of the square. In an applied way, however, where approximation is necessary, this can be done. The process takes on a symbolic importance in that it transfers the mysterious world of the irrational, ineffable, and incomprehensible to this world.

 There is an additional layer of meaning to the squaring of the circle process, which involves the moon. This is probably one of John Michell's most famous insights. The square drawn round the circumference of the earth which then produces a second circle with a circumference equal to the square's perimeter is just the right size to include the radius of the moon. By a strange natural coincidence, the square that is drawn around the circle representing the earth has the same perimeter as the circumference of a circle that has a diameter equal to the diameter of the earth plus the diameter of the moon.

  The moon's equatorial diameter is exactly 2 160 miles, or 1.738.1 km (Wikipedia). With the mean earth's diameter as 7 920 miles, this gives a total of 10 080 miles. All these numbers are multiples of 9, 2160 is 240 x 9, 7 920 is 880 x 9 , and 10 080 is 2 x 7 x 80 x 9. Previously the 864 / 275 approximation for pi was used to obtain the mean diameter of the earth in relation to a circumference of 24 883.2 miles (which is just over two miles of the current estimate). Here we now use 22/7 for pi. A circle with a diameter of 10 080 miles, representing the joint diameters of the earth (mean) and moon (equatorial), and pi as 22 / 7, the circumference is 31 680 miles. This is the significant number 3168 multiplied by 10.

   If we were to use today's value for the earth and moon sizes, and the approximation for pi given by a calculator, we would obtain 31 666.866 miles. The mean radius is given as 6371.0 km or 3 958.75586 miles (Wikipedia), so the diameter is twice that.

(3 958.75586 + 2 160) x π = 31 659.43680

This is also very close to 190 000 / 6 = 31 666.66667, and interesting possible connection to the Metonic cycle of 19 years, and 6, the all important and perfect number of ancient metrology. The number 31 680 is in fact 190 080 / 6. The number 190 080 is also important and a multiple of 9, being 10 x 33 x 64 x 9. This number 190 080 is also linked to the sun: the diameter of the sun can be roughly approximated by 19 008 000 / 7 miles, and the diameter by 19 008 000 / (7π).

   The sun's equatorial radius is given as 6.957 x 10⁸ m today (Wikipedia), which is 432 287.9384 miles. It was once thought of as 432 000 miles, another important number in the ancient system. The circumference then becomes 2 716 145.2232 miles (with today's values) or 2 715 428.571428 miles with the ancient value, which is also 19 008 000 / 7 miles.

   In the system described by Michell, we can see that it is important to round up or down to the closest multiple of 9, and that variations on approximations of pi can achieve this.

Another possible squared circle at Stonehenge

While looking at a Thom's dimensions for Stonehenge, I saw that the diameter of the Aubrey circle could be interpreted as 1920 x √π inches, which made me wonder if there was a squaring of a circle at work here too, not by circumference but by area. When a circle of area π is "squared", the resulting square will have sides of √π. The Aubrey circle is the largest circle withi n the earthwork circle, and consists of 56 post holes. The Aubrey circle is the one in yellow in the diagram here. Thom gives 86.44 metres for the diameter.

There are many possible interpretations of course, because of the size of the stones, there are multiple ways of measuring the distances between them. Also, because there has been movement over the centuries, with some stones having fallen and been re-erected for example, we have to work with a fairly high margin of error. No two people can be expected to take the same measure between two stones. The Aubrey circle could be interpreted as 520 Egyptian royal cubits for example. Or 19 / 7 metres, a reference to Robin Heath's silver fraction, or echoes of the sun's circumference in miles. There are many other excellent interpretations.

In this interpretation, the Aubrey circle is represented in yellow and measures 1 920 x √π = 3 403.1114 inches.

Below, this interpretation is shown against a plan of Stonehenge.

The starting circle, in purple, seems to go through some features on the plan.

Squared circles and astronomy

I also experimented with approximating a lunation in days, and a lunar year by squaring circles, as the diagrams show below.

This process works a little bit like the Eye of Horus multiplication, 63/64. You input a number and the output is slightly less. So here we input 360, the function is x √2 x π x √π / 8, and the output is 354.36622. If we input 64, the output would be 62.99844, very close to 63. We could use this function also for example for the number 432, if we input it into the function, we get an output of 425.23947, and we can then take the square root of that, and get 20.621335, which, in inches, is an acceptable Egyptian royal cubit. the function also bridges the Arab and French feet, so if we input 12.8 inches, the output is 12.599687 inches.

The lunar year can also be approximated in a simpler way, as below, but with a slightly greater margin of error. Above the result was 354.36622, and below it is 354.49077. A lunar year is 354.36708 days.

Squared circles and metrology

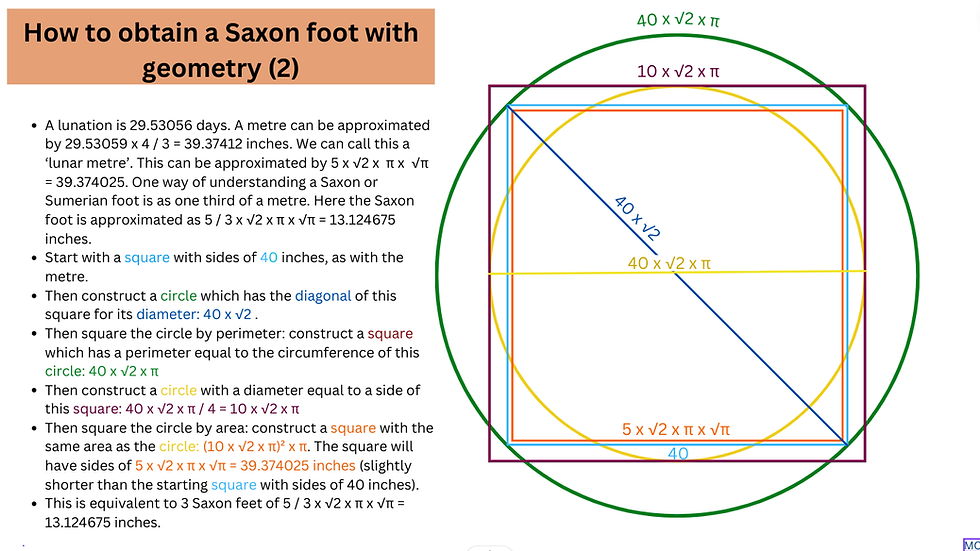
A metre is 39.3700787402 inches (or 10 000 / 254 inches). Historically, until the late 19th century, an unofficial 39.375 inch metre was important in the study of metrology, which is close to 29.53059 x 4 / 3 = 39.37412. The diagram below shows how to obtain this value.

Below are two possible ways to approximate an Egyptian digit in inches. Sixteen such digit approximate a Roman foot, 18 make a Sumerian or Saxon foot, 20 a remen and 54 a metre of 39.366 or 39.375 inches.

The diagram below shows how to approximate a Saxon or Sumerian foot of 13.2 inches.

The diagram below shows an approximation of a Saxon foot based on 18 digits of 0.72916667 inches.

Other units could be approximated in similar ways, for example an Egyptian royal cubit of 20.6165 inches by:  2.618034 x √2 x π x √π, or a Roman foot by 40 / 27 x √2 x π x √π inches, or a mile by  700 000 / 87 x √2 x π x √π inches.

Giza Connections

We can also use this geometric function to link parts of the Giza site.

Conclusion

The exploration of squaring circles, whether through ancient metrology or astronomical phenomena, reveals a fascinating intersection of geometry, mathematics, and symbolism. While these constructions may not provide exact solutions, they offer intriguing approximations that reflect the sophistication of ancient practices. From John Michell's insights at Stonehenge to the various ways of approximating lunar cycles and historical units of measure, these geometric methods underscore the enduring human quest to understand and symbolise the world through mathematical relationships. Though speculative, these connections invite us to appreciate the blend of precision and approximation that has shaped our understanding of the universe across different cultures and epochs.