68. Overview of the Moon's Role in the Giza Measures and Proportions
- M Campbell
- Jan 9, 2024
- 64 min read
Updated: Jun 11, 2025

There are many layers of complexity in the Giza design. Much amazing research has uncovered compelling metrological and geometric connections. This is an overview of the lunar connections in the Great Pyramid, the other Giza pyramids, and their layout at Giza. The Giza plateau has been precisely measured, and is obviously the work of highly skilled and sophisticated architects and builders. Here the dimensions given by Flinders Petrie are used. Many of the finds presented here are by Dennis Payne, his work can be found here on his Academia page. Thanks to Dennis for letting me use his diagrams here.
Encoded lunar cycles and periods
The following numbers correspond to lunar periods, cycles, and connections to the solar year.
Primary Numbers
Number of days in an average luntion: 29.53059
Number of days in a lunar year (12 lunations) is 354.36708
Number of days in a draconic month: 27.2122
Number of days in a lunar sidereal month: 27.32167
Number of days in a draconic or eclipse year: 346.620075883
Moon's sidereal rotation period in days: 27.321661
Number of lunar months in a Metonic cycle of 19 years: 235
Number of lunar months in an 8 solar year Venusian cycle: 98.946, almost 99
Number of lunations in a Halley Saros cycle: 223
Number of days in a Le Gentil Saros cycle: 1296 (1)
Number of days in a solar year multiplied by number of days in a lunar year / 100: 1294.298
Possible number of lunations in a solar year: 12 or 13
Average number of lunations per year: 12.3682662
Average number of lunations per year, approximated by: π x √3 x 100 / 44 = 12.36681
The number of days difference between the solar and lunar years: 10.875119
Number of lunations in an Egyptian cycle of 25 years of 365 days: 309
Number of days in this 25 year cycle: 9125
309 + 309 = 618, approximately equal to 1000 phi (Guyla Priskin)
Number of days in a week: 7
Number of weeks in a month: 4 (plus 1 day remainder)
Number of lunations in a 600 year period: 7,420.9597
Number of days in moon apogee cycle (Le Gentil): 248 (2)
Equatorial radius of the moon in miles: 1080
Average number of months per traditional Hebrew calendar year = 235/19, so the number of years in the molad moment repeat cycle = 25920 / (235/19) = 2095+31/47 years. Every 18 months the molad moment is exact to the minute with zero parts remaining. Every 1080 months or 87+7/22 years the molad moment is exact to the hour with zero minutes and zero parts remaining. (3)
Number of months in Hebrew calendar complete molad cycle: 25920 (4)
Number of divisions or parts (chalakim) in an hour in Hebrew Calendar: 108 (5)
Number of chalakim in a 24 hour day: 2592
Number of years in ancient Persian cycle: 1440. (13)
Number of years in Tartar ancient cycles mentioned by Jean-Sylvain Bailly in his History of Astronomy: 60, 180 & 10,000. (14)
Secondary Numbers
Lunar pi and 864. A lunation can be related to this number associated with the sun, together with pi as 22/7, and the difference in days between a solar and lunar year, 10.875119. Lunar pi: 29.53059 x 1000 / (10.87512 x 864) = 3.142855
Lunar pi 2: 365.242199 x 254/ ( 29.53059 x 10 000) = 3.1415396. This is because 2.54 cm are 1 inch, and the average number of lunations in a solar year (365.242199 / 29.53059 = 12.368266), if taken as a measure in inches, converts to 0.31415396 metres.
Lunar pi 3: 12.36681 x 44 / (√3 x 100) = 3.141591676, with 12.36681 as the average number of lunar months in a year of 365.242199 days. The lunar month to solar year ratio is in fact very close to π x √3 x 100 / 44. = 12.36681, and 365.242199 / 29.53059 = 12.368266. Pi, the square root of 3, and 440 are all important numbers in the Great Pyramid.
Metonic pi 2: 365.242199 x 19 / 47² = 3.1415128
Metonic pi 3: 29.53059² x 25 / (19 x 365.242199) = 3.1415915
Metonic pi 4: (365.242199 / 354.36708 x 2 x 254 / 1 000) + (√5 + 3) / 2 = 3.1416239
Soli-lunar Phi: 76 / 47 = 1.61702127 and 29.53059 x 20 / 365.242199 = 1.6170415
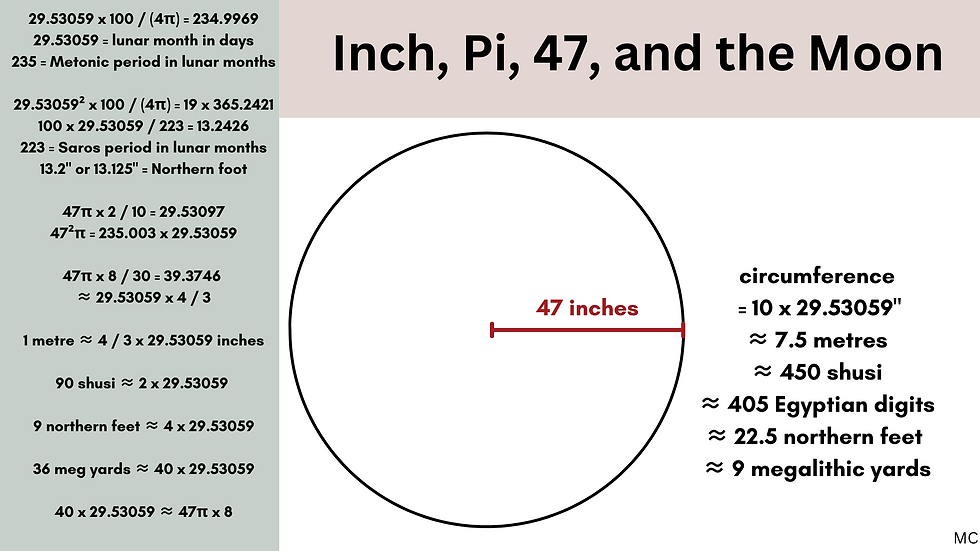
Lunar √2: (47 x 8)² / 10 000 = 1.41376, or (5/(4 x 47))² x 2000 = 1.414667. And 1.41376 x 10 000 π x /(47 x 32) = 29.53097. Or with Metonic pi, the result is 29.53022.
47: A number associated with lunar cycles expressed though geometry, found by Jim Wakefield, and also Dennis Payne.
600 years also provide an interesting link to a lunation and pi: 600 x 365.242199 = 12 x 29.53059² x π x 20 / 3
Lunar √3 #1 : 29.53059² x π x 40 /( 3 x 365.242199 x 346.62) = 1.73121
Lunar √3 #2: Phi x 235 / 223 x 4 x 254 / 1000 = 1.73238442 ≈ √3
Three complete lunar orbital cycles (or transits past the same star) in days (3 x 27.32167 = 81.96501): 82 (8)
1 lunar sidereal period multiplied by 366: 9999.73122, or with rounded up figures 82 x 366 / 3 = 10 004 (9)

Units used:
Inch: an inch generally represents a day. It is possible that the inch used at Giza, if it was used at Giza, was very slightly different to the modern inch. This is to be expected, when even in the last century or so, the inch has been modified slightly, so it stands to reason that over thousands of years there may be a slight discrepancy with today's value. The modern inch is in fact slightly different to the inch used by Flinders Petrie in his Giza survey. In a 1911 article, Flinders Petrie gives the value of the metre in inches of the time, as 39.370113 inches, in Great Britain, and as 39.37 inches in the United States measure of the day, in keeping with the 1897 Weights and Measures Act. In 1928, in a paper entitled "A New Determination of the Ratio of the Imperial Standard Yard to the International Prototype Metre", by J.E. Sears, W.H. Johnson and H.L.P. Jolly, the metre is defined as 39.370147 inches. By 1930, the British Standards Institution defined an inch as 25.4 mm, based on the metre, so a metre was worth 39.3700787402 inches. The Commonwealth Science Congress confirmed this is 1946, acknowledging that the yard was 1.7 millionths of an inch longer than the old imperial inch, and 2 millionths of an inch shorter than the old US inch. The international inch has been exactly 25.4 mm since July 1959, and since then the international yard has been 0.9144 metre. The American inch was changed by 2 millionths of an inch and the UK inch by 1.7 millionths of an inch. The difference in inch proposed here is in the region of 1.0002766, which seems to align the astronomical time cycles as measured in days with the measures in inches, meaning that the measures found by Flinders Petrie can be divided by 1.0002766 to approximate more closely various astronomical cycles such as a lunation in days.
Egyptian royal cubits: values range from 20.625 inches, to near 20.619, 20.6181818 inches, and 20.614 inches. When taken as values in inches, these cubits make sense in terms of sun and moon cycles. For example 20 x 365.242199 / 354.36708 = 20.613777. Or for example 990 lunations is the approximate equivalent of 80 years, and 48 lunations multiplied by the ratio between the solar and lunar years and then 20 is approximately equivalent to 990 lunations, and 990 divided by 48 is 20.625. These 48 lunations also reconcile 80 solar years with 20 x the ratio between the lunar and solar years. So 20.625 x 365.242199 x 80 / (990 x 29.53059) = 20.613777. The 20.6193 inch cubit is what we get when we divide the width of the Giza rectangle as measured by Flinders Petrie, 29 227.2 inches, by 48 lunations (48 x 29.53059). A 20.625 inch cubit relates to the metre via Phi and 2, so that with 39.375 inches for the metre, 39.375 x 2/10 x 55/21 = 20.625. And if we multiply 20.6193 by the conversion factor of 1.0002766, the result is 20.625, suggesting that a theoretical 20.625 inch cubit (the number 20.625 being the important element) can perhaps be interpreted on the ground as 20.6193 inches.
This suggest that the inch used at Giza can be read slightly more easily in terms of astronomical cycles if we divide the measures on the ground by 1.0002766, or multiply the astornomical numbers of days by this number. Perhaps this ratio represents the difference between our modern day inch and an older inch used at Giza, and may also take into account any difference in the actual or measured length of the lunar, solar, and other cycles at the time of the pyramids' initial design.
Metre: the metre as a measure in inches relates to the cycles of the sun and moon, with 39.3700787402 x pi / 10 being equal to the average number of lunations in a year. The metre in inches, 39.3700787402, multiplied by 76 x pi / 200 is very nearly equal to 47. The metre in inches is very close to the number of days in a lunation multiplied by 4/3, this fraction linking the Chaldean / Babylonian 60 year period with the 80 year period, which is 40 Olympic periods, and 10 cycles of Venus. 600 years are 7420.9557 lunations, almost 7421, and 80 years are 989.461 lunations, almost 99. 1 inch is 2.54 cm. The number 254 is lunar, in that, in a Metonic cycle, of 235 lunations, or 19 years, there are also, approximately, 254 sidereal months of 27.321 days.
Roman foot: as 11.664 inches.
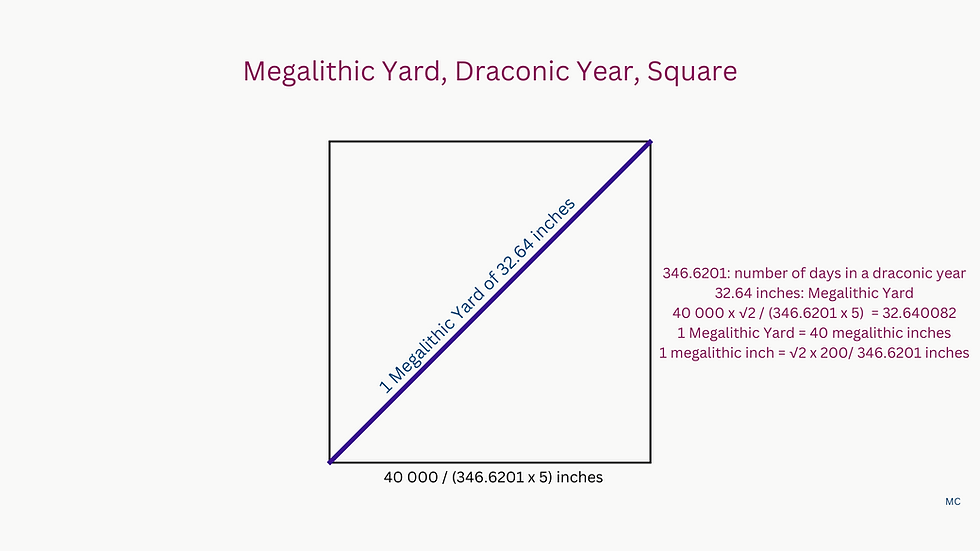
Megalithic Yard, as 32.64 inches. The Megalithic yard at Giza links the solar year, the 8 year cycle of Venus and the draconic year, as 8 x 10 000 / (346.6201 x 5 x √2) = 32.6401, which is the number of inches in a Megalithic Yard. This in turn can also be linked to one of Richard and Robin Heath's interpretations of the Megalithic Yard expressed in inches, as 3 times the difference between the solar year and the lunar year. (365.242199 - 354.354.36708) x 3 = 32.625357 inches. (8) In geometric terms, as 32.64 is almost exactly 80 000 / (5 x 346.6201 x √2), we can say that a square with sides of 32.64 inches each, in other words 1 Megalithic Yard, has a diagonal of 80 000 / (5 x 346.6201) inches, representing the ratio between 80 000 days and 5 draconic years. Or if we re-write it as 40 000 x √2 / (346.6201 x 5) = 32.64, then a square with sides of 40 000 / (346.6201 x 5) inches will have a diagonal of 1 Megalithic Yard. With 40 megalithic inches in one Megalithic Yard, then 1 megalithic inch can be equated with √2 / (5 x 346.6201) inches.
The megalithic yard can also be defined as 40 x √2 / √3 = 32.65986 inches (David Kenworthy) or 82.944 centimetres (Quentin Leplat).
Saxon or Druisian foot. This is 13.2 inches.
Analysis of Giza Site
1. The Great Pyramid (interior)
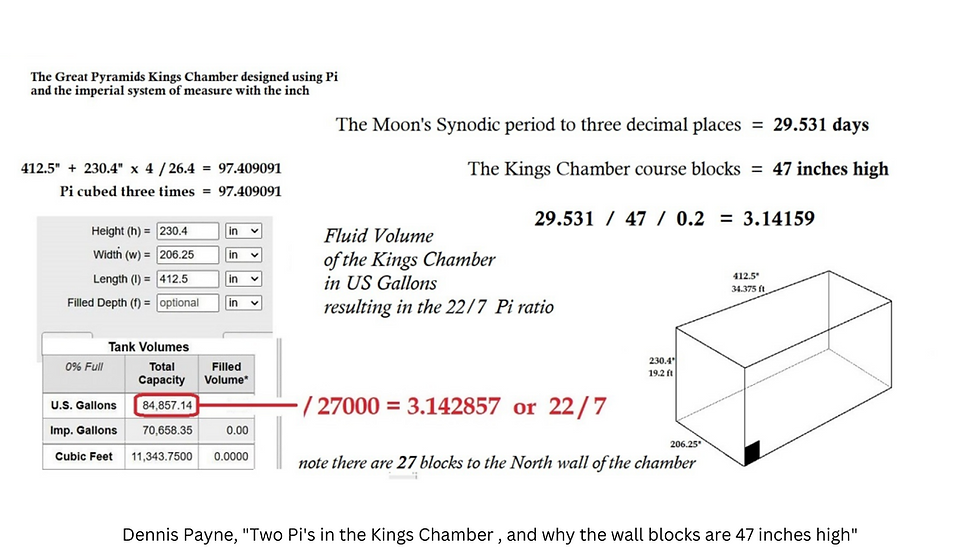
The King's chamber dimensions given by Flinders Petrie are: King’s Chamber mean length (N) 412.40 King’s Chamber mean length (S) 412.11 King’s Chamber mean width (E) 206.29 King’s Chamber mean width (W) 205.97.
The king's chamber can be interpreted as linked to pi, to phi, or to the moon: as 10 pi metres: 10 π = 31.415927, as 2 000 phi inches: 2 000 x 0.61803 = 1236.06, or in a lunar way in metres: 354.36708 x 3 x 29.53059 / 1 000 = 31.39401.

The chambers located above the king's chamber can also be interpreted in terms of the moon. The dimensions in inches are:
Chamber above King’s 1st N | 460.80 |
Chamber above King’s 1st E | 205.80 |
Chamber above King’s 1st S | 464.60 |
Chamber above King’s 1st W | 205.90 |
Chamber above King’s 2nd E | 204.65 |
Chamber above King’s 2nd S | 471.80 |
Chamber above King’s 3rd N | 479.00 |
Chamber above King’s 3rd S | 472.00 |
Chamber above King’s 3rd W | 198.00 |
Chamber above King’s 4th N | 481.00 |
Chamber above King’s 4th E | 196.00 |
Chamber above King’s 4th S | 467.00 |
Chamber above King’s 4th W | 198.00 |
Chamber above King’s top N | 462.00 |
Chamber above King’s top S | 468.40 |
Chamber above King’s top W | 247.00 |
Chamber above King’s 1st N | 460.80 |
The first chamber N can be read as 3/2 x 7.8 metres, or 460.6299 inches, which references the 780 days in a Mars cycle. The second chamber east, 206.65 inches, can be read as 354.36708 / √3 = 204.5939 inches.
The height of the mouth of the passage out of the king's chamber is 29.4 inches, which is close to 18 π x 9 / (10 x √3) = 29.38355, a megalithic yard x 9 / 10. Or could even be compared to 29.53059 inches.
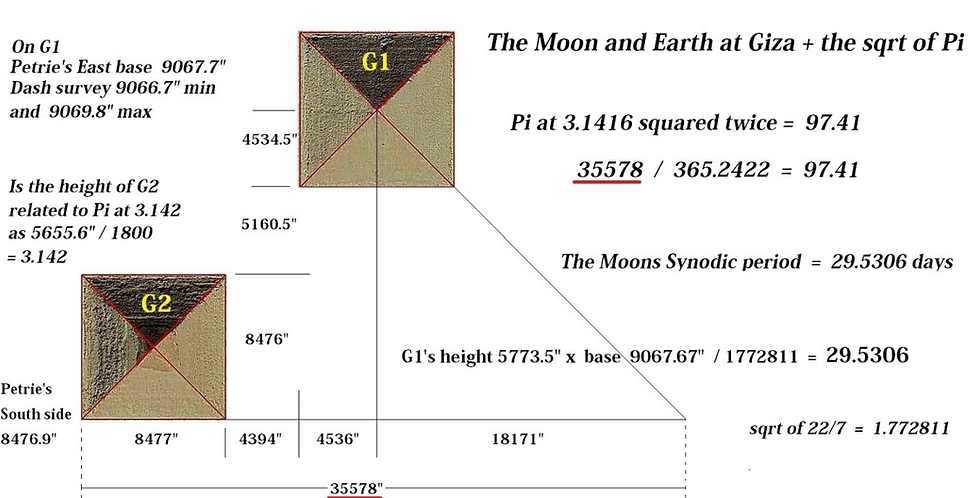
Dennis Payne, using Piazzi Smyth's figures for the wall block heights of 47, has made the connection to the moon. The number 47 is linked to the number of days in a lunation and pi. See his diagram below.
2. The Great Pyramid (exterior)
Great Pyramid height 5776.0 ± 7.0
Great Pyramid mean Case Plane Sides 9001.5
Mean socket sides 9125.9
Mean side of "of the original base of the Great Pyramid casing on the platform" 9068.8 (7)
The main dimensions of the pyramid's exterior can be understood as expressions of the ratio between the solar and lunar year, in inches, or alternatively as derived from approximately 10 000 inches, then, in either case, divided by the square root of three, multiplied by pi, Phi, etc.
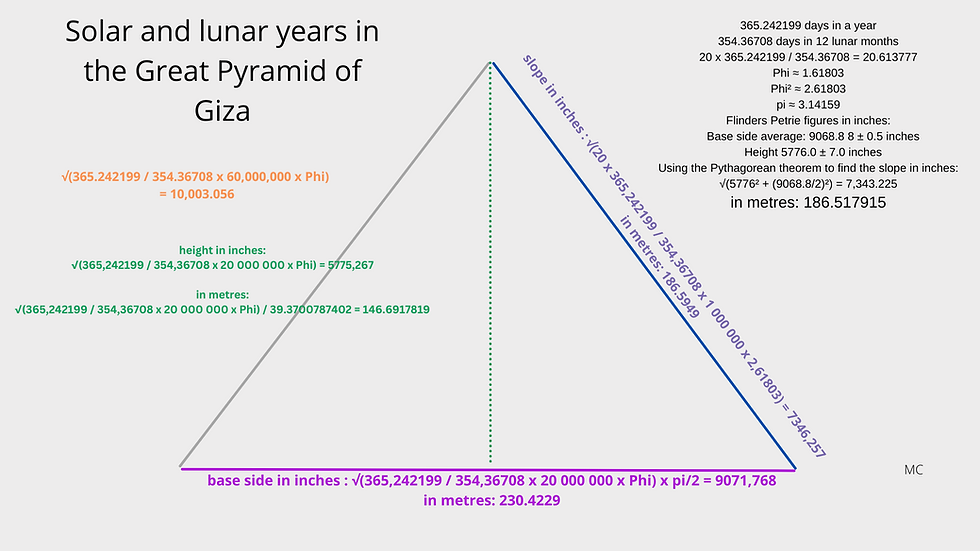
The height
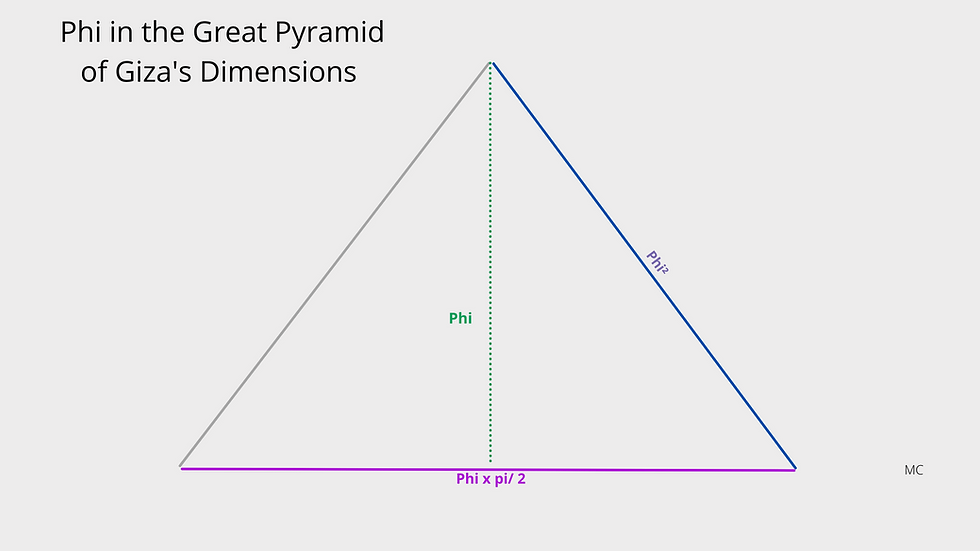
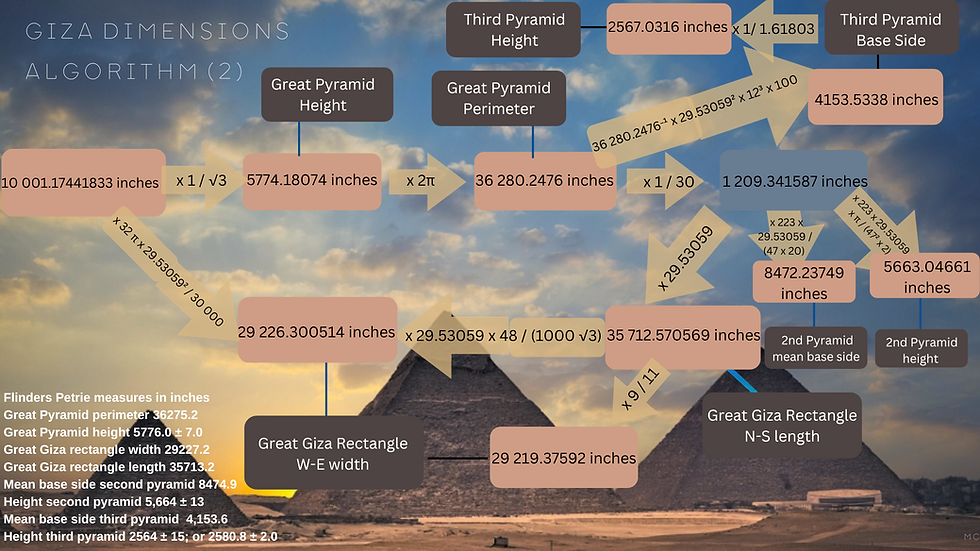
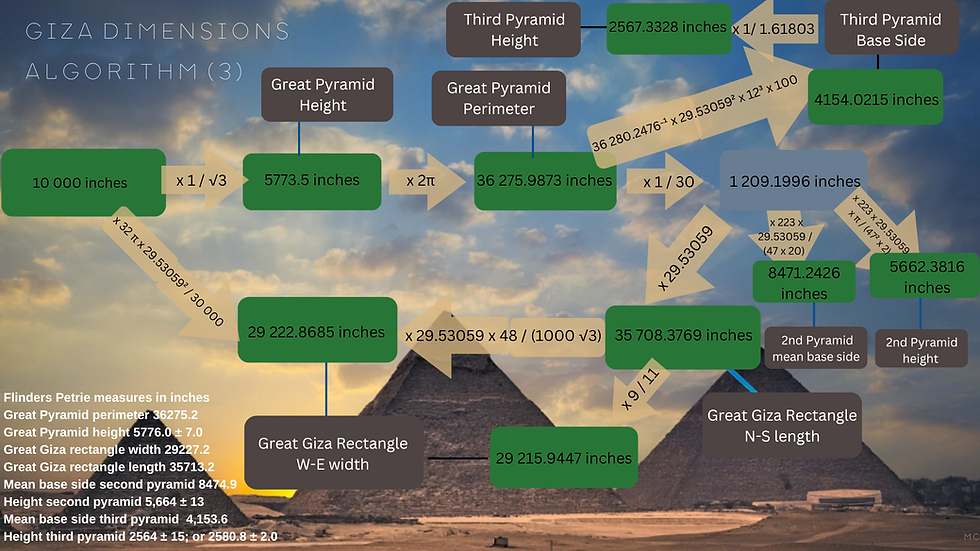
The height is given as 5776 inches by Flinders Petrie, and this could be interpreted as √(365.242199 / 354.36708 x 20,000,000 x Phi) = 5775.267 inches, involving the solar and lunar years in days and Phi, the golden ratio, 1.61803.
Or it can be interpreted as 10 000 / √3 = 5773.50269 inches. The 18th century French astronomer Jean-Sylvain Bailly mentions an ancient cycle of 10 000 years, used by the Tartars, which was used in combination with cycles of 60 and 180 years. Alternatively, a figure just above or below 10 000 also produces a height within Flinders Petrie's error margin. As Robin and Richard Heath explain in their work on Le Ménec in France, 10 004 is 27.3333 x 366, that is a rounded up sidereal period multiplied by 366. Or 27.32167 x 366 is 9 999.73. At Le Ménec, Richard and Robin Heath write that"a 10,000 inch length was purposely generated at Le Menec as the perimeter of Le Menec’s distinctive egg shape", adding "there are almost exactly 10 000 chronons in the average lunar orbital period." (9) The same system could have been used at Giza, and certainly the use of the day inch, and even the megalithic yard at Giza, suggest strong connections with megalithic France and the UK.
28 / 10 000 is a good approximation of 3√3/ (20 x π x 29.53059). There are 280 Egyptian royal cubits in the height of the Great Pyramid. So the height of the Great Pyramid can be interpreted as 3√3/ (20 x π x 29.53059) x 2 000 000 x 365.242199 / 354.36708 = 5772.81266 inches, which simplifies to √3 /π x 300 000 / 29.53059 x 365.242199 / 354.36708, and if multiplied by √3 is 9 998.8048, close to 366 sidereal months of 27.32166 days.
The height can be connected to the draconic year. Dennis Payne has made the connection between the draconic year and the height of the Great Pyramid via the number 100 / 6. This may provide a compelling reason to explain the connection to the square root of three here, as it may be a way of interpreting geometrically the draconic year. The space diagonal of a cube (the line connecting two opposite corners of a cube), and the height of an equilateral triangle are both √3 units, when the sides are 1 unit. There are 346.6201 days in a draconic year, and 346.6201 x 100 / 6 = 5777.001667. This is very close to 10 000 / √3, and indeed 5777.001667 x √3 is 10 006.0604. As a measure in inches, 5777 is within Flinders Petrie's error margin for the height of the Great Pyramid. Also, 5 draconic years in days are 1 733.1005, which, divided by 1000, is close to the first few digits of √3, which are 1.73205.
There is a connection to the length of the Queen's Chamber within the Great Pyramid here. The length is given by Flinders Petrie as 227.5 inches, which is equivalent to 5.7785 metres. So if the height of the Great Pyramid is interpreted as 10 000 / √3 inches, the floor length of the Queen's Chamber is 10 / √3 metres.
The height in inches (and by extension the length of the Queen's Chamber in metres x 1000) can be related to 200 x pi x Phi x 29.53059 / (3 x √3) = 5777.7225. So the 10 000 inches that are then divided by the square root of three are also linked to this equation: 200 x pi x Phi x 29.53059 / 3 = 10 007.31.

The height as 10 000 /√3 inches could also simply be referencing a period of 10 000 years. Bailly writes: "The Tartars confirm the antiquity of the time of Fohi, or at least go back to this period. They count in cycles of 60, 180 and 10,000 years, the number of which encompasses a prodigious number of years."(14)
As Howard Crowhurst points out (15), the number of hours in a lunation multiplied by 127 and divided by 9 is very close to 10 000. 29.53059 x 24 x 127 / 9 = 10 001.02648. So the height of the Great Pyramid in inches could be interpreted as 29.53059 x 24 x 127 / (9 x √3) = 5774.0953. This could be simplified to 29.53059 x 4 x 254² / (√3 x 30 000). Since 29.53059 x 4/3 is close to 10 000 / 254, we can then also think of the height in metres simply as 254 / √3 = 146.64697.
The height can also be interpreted by multiplying any of the interpretations for the base side of the Great Pyramid by 2/π.
2. The slope
The height and the slope are in √Phi ratio. The slope of the pyramid then becomes √(365.242199 / 354.36708 x 20,000,000 x Phi²) = 7,346.26086 inches.
Or 10 000 x √(1.61803 / 3) = 7343.9998 inches.
3. The base
The height and base are in pi/2 ratio, so the base becomes √(365.242199 / 354.36708 x 10,000,000 x Phi x π). The ratio between a solar year and lunar year that can be found in the 20.613777704 inch cubit returns here, and perhaps refers to the solar and lunar values found in the Giza rectangle itself. (365.242199/(29.53059 x 12) x 20 = 20.61377705)
The side can also be interpreted, in inches, as 5 000 π / √3 = 9068.9968. The fraction π / √3 can be considered lunar because it links key lunar and solar time cycles, as periods in days (see below).


The Great Giza rectangle, encompassing the outer corners of the Great and third pyramids, has a width close to 2/3 x π / (29.53059 x 4)² inches and a length of close to 2 π / (√3 x 3) x 29.53059 x 1 000 inches, and if multiplied by 30 / 29.53059, gives the perimeter of the Great Pyramid, which is almost equivalent to multiplying the length by 254 / 1000 (ratio between metre and inch) to obtain a side of the Great Pyramid.
Another way interpreting the Great Pyramid side is then 3 000 / 4 x 365.242199 x 346.62 / (354.36708 x 29.53059) = 9073.5666 inches, though it is a little on the big side.
The side is also close to 365.25² x √3 x π x 15 00 000 / (108 x 432 x 29.53059³) x 1.0002766 = 9065.222
The base side as 230.338602 metres is also 29.53059 x 52 x 3 / 20, with 52 being the number of weeks in a year, or alternatively, 29.53059 x 3 x 364 / 140, the 364 being sometimes given as the number of days in a year, as per the Book of Enoch for example. 230.338602 metres are 9068.4487 inches, well within Flinders Petrie's margin, or 29.53059 x 7.8. Two sides together, or 230.338602 x 2, are 156 lunations in days, expressed in metres, but also 4 606.77204 metres. This is close to an important number in metrology, as various units are derived from it, such as the vara as 4.608 / 6 = 0.768 metres and the Assyrian Royal cubit as 4.608 / 7 = 0.6582857 metres (see the work of C. Mauss). To within a small margin of error these units can be linked to the number of days in a lunation expressed in metres, the vara as 156 x 29.53059 / 6000 metres and the royal Assyrian cubit as 156 x 29.53059 / 7000 metres. Coincidentally, 230.34 is the number of inches in the height of the King's chamber, as pointed out by Dennis Payne, and so the same lunar associations can be made there, but in inches instead of metres. Stephen Dail has observed that Petrie noted the use of a cubit of 20.607 inches in the height of the King's Chamber, and that this cubit corresponds to the cube root of 8750, which, multiplied by √125, gives 230.39326 inches.
Another interpretation of the base side is with a value of 9067.5311 inches, equivalent to 365.242199 x 12 x 223 x 29.53059 x π / 10 000. This brings in 223, the number of lunations in a Saros cycle (Halley's Saros of 223 lunations, not the Babylonian Saros).
Another interpretation is this: the 600 year period known to the Chaldeans and ancient Brahmins is 7420.9597 lunations of 29.53059 days. So that, approximately, 7421 x 29.53059 = 600 x 365.242199. The 7421 days, multiplied by 11 / 9 are 9070. As a measure in inches, 7421 x 11 / 9 = 9070.1111, or 11 / 9 x 7420.9597 = 9070.06, very close to the base side of 9068.8 inches. The 11 / 9 fraction can also be seen in the ratio between the width and length of the great Giza rectangle. Base = 7421 x 11/9 =9070.111 inches. As we will see, the width of this rectangle in meters is also close to 742.1 (or 7,420.9597 x 1.0002766 / 10 = 742.3012 m, using the coefficient 1.0002766 to bring the astronomical values closer to Flinders Petrie's measurements).
With the mean side of the Great Pyramid as 5 000 π / √3 inches, and the perimeter of the Great Pyramid as 20 000 π / √3 inches, we can arrive at a number close to the number of days in a lunation with pi, the square root of 2, and 47.
Taking a slightly reduced value for the mean base side, as 9065.9713 inches, the diagonal of the square base is 12 821.218 inches. This is equivalent to 47 x 2 units of 136.39595 inches, or 47 x 2 x 29.53059 x √3/3 x 8 inches. The circumference of the circle drawn with a radius of 47 x 2 x 29.53059 x √3/3 x 8 inches is 29.53059² x √3/3 x 80 inches (using 29.53059 x 5 / 47 for pi). The base side as 9065.97 inches can be thought of as 47 x 2 x 29.53059 x 8/3 x √3/√2 inches. Dividing the radius of any circle into 47 units always allows for ten lunations to be expressed in the circumference, in that same unit, and the number of days in a Metonic cycle in the area, in that unit, squared. This works because, pi works with the number 47 to produce the number of days in both a lunation and a Metonic cycle, and an approximation of pi in Metonic terms is 365.242199 x 19 / 47², to about 99.99746 % accuracy. The number 19 is the number of years in a Metonic cycle, and the number 47 multiplied by 5 is the number of lunations in a Metonic cycle.

Another interpretation for the base side involves the Mars orbital period in days and the lunation, also in days. The synodic orbital period Mars is 779.94 days (close to 780). With 779.94 / 10, we get 779.94 / 10 x 29.53059 = 230.32088, which is the value of the base side in metres, equivalent to 9067.75132. Or rounding the Mars period up, we get 780 / 10 x 29.53059 = 230.3386 for the measure in metres, equivalent to 9068.4489 inches. The metre seems to express lunar cycles in conjunction with other cycles, such as Mars, here, or in the Great Giza Rectangle, Venus. The sidereal orbital period for Mars is 686.980 days. If we take 9068.4489 inches for the Giza base side, this is 13.2 x 687, that is 687 Saxon feet. So we can think of the ratio between the metre and the Saxon foot in terms of Mars and the Moon, as approximately 687 x 29.53059 x 100 / 780.
Another interpretation is in terms of the Persian / Assyrian foot of 12.96 inches, or 12 x 12 x 16 / 7000 metres of 39.375 inches. There is a soli lunar cycle of 1296 days, from the Chaldean and Indian traditions, written about by Le Gentil, which he terms "Saros" (not the same as Halley's, and our modern day Saros), or 3.6 years of 360 days. (See his Voyages dans les Mers de L'Inde Tome 1 p 339, see in Notes. The Giza base is 700 such feet.
The number of lunations in a year, on average, can be approximated by this fraction: π x √3 x 100 / 44 = 12.36681. So that even pi and the square root of three can be considered lunar. The 440 cubits present in the mean base side of the Great Pyramid can also be related to this equation. And the mean base side of the Great Pyramid can be understood as π x √3 x 10 000 / 6 = 9068.9968 inches. If the base side is π x √3 x 10 000 / 6 inches, the average number of lunar months per year can be understood as base side in inches x 6 / 4400 = 12.36681. In this way 440 can be understood as a lunar number, and also 44 lunar years are approximately 45 draconic years. The base is also 365.242199 / 29.53059 x 10/6 x 440 = 9070.0619 inches.
Both the side and the height can be linked to the mean number of lunations per year. 12.368266 x 4400 / 3 π = 5774.18074 Great Pyramid height in inches, and the side is then 12.368266 x 2200 / 3 inches, or 300π / (√3 x 44) inches.
235 lunations in a Metonic period, and also 254 sidereal months. The side of the Great Pyramid can be interpreted as 254 × 29.53059 × 2π /(3 x √3 ) = 9,069.9277 inches. The height is then 254 / √3 x 29.53059 x 4/3 inches, and since 4/3 x 29.53059 inches is close to a metre, we can also say that it is 254 / √3 = 146.6470 metres high. There are 10 000 / 254 inches in a modern metre. 254 x 29.53059 x 4/3 = 10 001.0265
In metres, the side of the Great Pyramid is 254 π / (2 x√3) metres. But we can also think of it as √2 / √3 x 100 000 / 354.36708 = 230.409828 metres, equivalent to 9071.253087 inches. If we understand the megalithic yard as √2 / √3 x 40 = 32.65986 inches, as put forward by David Kenworthy, then we can also interpret the side as 10⁸ / ( 4 x 254 x 354.36708) = 277.749267 Megalithic Yards. This is close to 2500 / 9 Megalithic Yards, as 354.36708 x 254 = 90 009.23832, very close to 90 000.
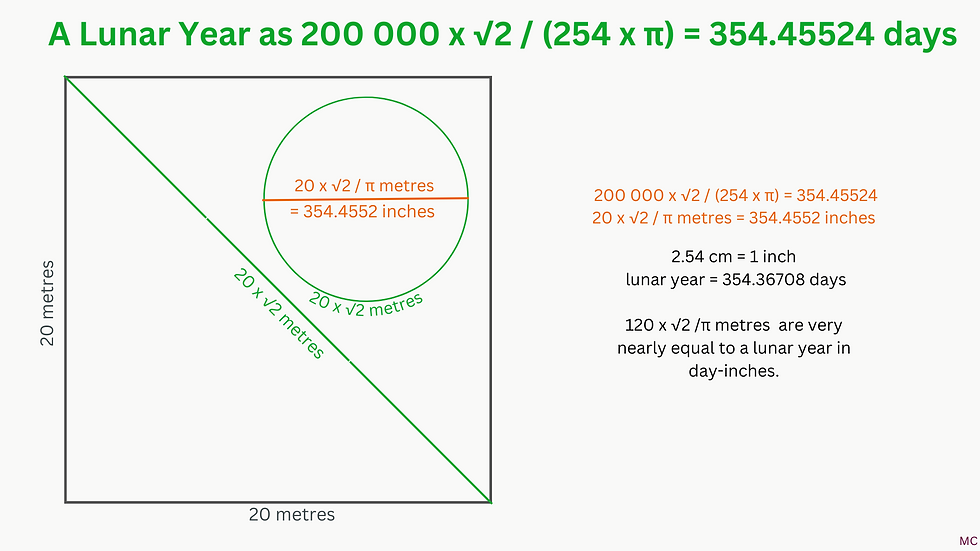
We can also interpret the side of the Great Pyramid as √2/√3 x 100 000 / 354.36708 = 230.40983 metres, equivalent to 9071.2531 inches. A lunar year is 354.36708 days. An inch is 2.54 cm. The existence of the metre owes a lot to the number 254, in its role with the inch as "day-inch". A lunar year can be represented geometrically as 200 000 x √2 / (254 x π) = 354.45524, which basically means that 20 x √2 /π metres are very nearly equal to a lunar year in day-inches. This is especially interesting when 20 cm x 2.61803, which is Phi squared, make a royal Egyptian cubit, as 52.3606 cm (20.6144 inches), and also, if we were to add a value of 2.61803 cm to this cubit in cm, we would obtain a nice approximation of pi, 3.141636. Furthermore, if we were to multiply that cubit as a value in inches by the number of days in a lunar year and divide by 20, we would obtain a nice approximation of the solar year in days: 20.6144 x 354.36708 / 20 = 365.2534. This gives a strong indication that the metre and the inch are both intimately connected to the Giza plan, and to each other.
Dennis Payne has found that the number of days in a lunation can be arrived at simply by multiplying the side, base diagonal, slope, the ridge and the height together, and dividing by 144 x 10⁸ inches.

David Kenworthy has found that 29.53059 x 144 is significant at Giza. The Egyptian royal cubit squared, as a unit of area, is 144 x 29.530598 square inches.
Dennis Payne has also found lunar connections between the height and base side of the Great Pyramid, multiplied together, and then divided by the square root of pi and 10⁶. This works also with calculator pi instead of 22 / 7, and slightly different measures, for example 5772 and 9068.193.
The base perimeter is close to 9!/10 inches, if we take 9068.8, as per Flinders Petrie, and multiply it by 4.
Another possible connection involves an equilateral triangle, with sides equal to the base side of the great pyramid, as 9069 or 9070 inches, and a possible link to Phi squared and the draconic month, with the square root of three, so the base side is 2.61803 x 2 x √3 x 1 000 = 9069.1220 inches.
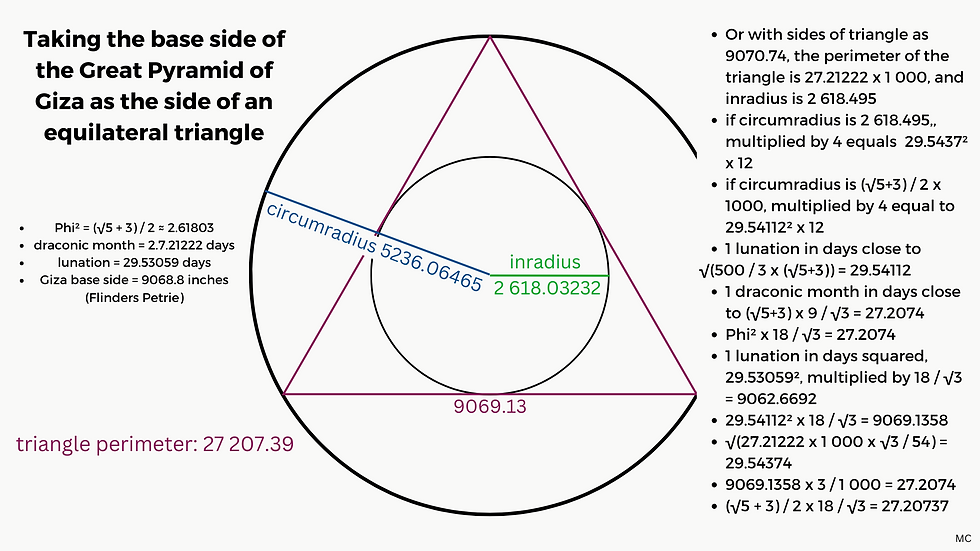
The value of the circumradius, here in inches, 5236, is equivalent to the value of an Egyptian royal cubit in metres.
So far, only the 9068.8 base side has been considered. But in fact the outer perimeter, running along the socket sides, is 4 x 9125.9 inches. The mean side of 9125.9 corresponds to the number of days in a 25 year cycle, with 365 days per year, approximately equivalent to 309 lunations. 365 x 25 is 9125. Four times this 25 year cycle is 36 500 days long, which is almost exactly 1236 lunations long also. This is 2 x 618, which offers a connection to phi, as Gulya Priskin has observed. Therefore the base perimeter is equivalent to 100 years of 365 days, which is approximately 2 000 x phi lunations. Here the astronomical value corresponds to the actual measure in inches.
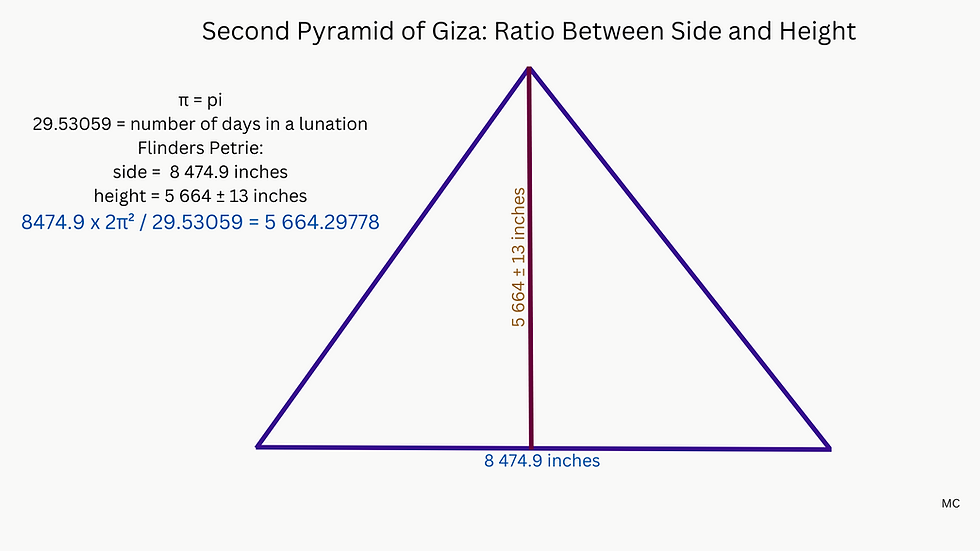
2. The Second Pyramid
Mean base side second pyramid 8 474.9
Height second pyramid 5 664 ± 13
Flinders Petrie gave the mean base of the second pyramid as 8474.9 inches. One side of the second pyramid can be interpreted as 411 cubits, 411 being a lunar cycle in days. The full moon cycle, the time it takes the sun, as seen from Earth, to complete one revolution with respect to the perigee of the moon’s orbit, is 411.784 430 29 days. 8474.9 / 411.7844 = 20.5809. This implies a cubit of 20.5809 inches. We can think of the side as 20 x 365.242199 / 354036708 x 411 = 8472.2624 inches, which, multiplied by 1.0002766 gives 8474.6058 inches.

The ratio between the side and the height can be interpreted as side x 2π² / 29.53059 = height. 8474.9 x 2π² / 29.53059 = 5 664.29778.
Both the height and base can be related numerically to the average number of lunations in a year. 12.368266 x 440 x 14 / 9 = 8465.39095 Close to base side second pyramid in inches.
The base side can be expressed in inches as 14 000 π / (3 x √3).
Or 223 x 38 = 8 474 inches, 223 being the number of lunations in a Saros period (Halley) and 38 being related to the Metonic period, as 365.242199 x 38 / 470 gives approximately the number of days in a lunation.
Or as 100 x π x 29.53059 x 223 / (47 x 3 x √3) = 8471.2426 inches, Multiplied by 1.0002766, this is 8 473.5858 inches, very nearly Flinders Petrie's measure. 223 x 29.53059 days is the number of days in a Saros period (Halley). Which means that the base side of the second pyramid in inches can be multiplied by 47 x 3 x √3 / (100π) to obtain the Saros period in days.
Another interpretation is 346.62 x 365 x 223 x 100 / (354.36708 x 47 x 20) x 1.0002766 = 8472.0836.
Or 346.62 x 365.242199 x 223 x 10 / (354.36708 x 47 x 2) = 8475.3610, which multiplied by 1.0002766 is 8477.7053. As 29.53059 x 47 is approximately equivalent to 3.8 x 365.242199, the side is also 346.62 x 223 x 10 / (24 x 3.8) = 8475.467, or with the factor of 1.0002766, 8477.8113. It is also close to 223 x 38 = 8474, and to 223 x 29.53059 x 470 / 365.242199, combining Metonic and Saros numbers (Halley), as there are 223 lunations in a Saros period, and the ratio between the year of 365.242199 days and a lunation in a Metonic period is close to 470 / 38.
Dennis Payne has found that two sides of the base, added to the diagonal of the base can be interpreted as a year divided by 800 expressed in miles. Mean base side second pyramid 8474.9. Two sides and the diagonal combine to measure 8474.9 x 2 + 8474.9 x √2 = 28 935.11852 inches. And 365.242199 x 5280 x 12 / 800 = 28 927.1822. The ratio between 28 935.11852 and 28 927.1822 is 1.000274356, very close to the coefficient being used in this study more widely, of 1.0002766, derived from the ratio between the lunar numbers associated with the Great Giza Rectangle and the measure in inches there.
The side of the second pyramid is also equivalent to 365.242199² x 100 / (√2 x 354.36708 x π) = 8473.1272, which, also can be then multiplied by 1.0002766, to make 8475.4709. What this suggests is that the diagonal of the second pyramid, as 8473.1272 x √2 inches, multiplied by pi, produces a circle with a circumference equivalent to 37 645.1127 inches, or (10 x 365.242199²) / 354.36702 = 37 645.113 inches. The side of the second pyramid can be interpreted as 354.36708 x 365.242199 / (40 x π x √2) Roman feet of 11.64 inches. Or as 365.242199 x 10 / (π x 2√2) = 411.0419 Egyptian Royal cubits of 20.625 inches, as mentioned above, referencing the 411 day lunar cycle.
It is interesting to note that the proportions of the Great Giza Rectangle, 9 x 11, are mirrored in the relationship between the side of the second pyramid, as 8475 inches, and the 19 year Metonic period, as 8475 / (19 x 365.242199) ≈ 11/9.
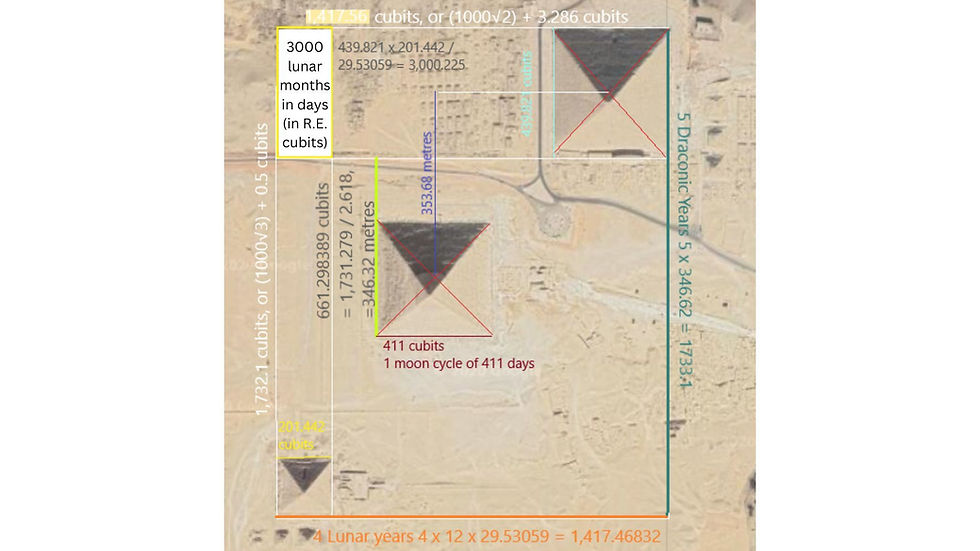
Below is a diagram of Dennis Payne's, showing the connection to five draconic years.

It's worth highlighting that, as Dennis remarks, the height of the Great Pyramid works out as 10 000 / √3 inches, and the second pyramid height works out as 4000 x √2 inches. This coincidence suggests that the inch was indeed used. It also suggests that the role of these irrational numbers was important, to the Giza designers. The third pyramid is about Phi, and the height multiplied by 1.61803 gives the base.
Dennis Payne's diagram below shows the connection between the slope, the ridge, and the lunar month. The values for the slope and ridge and inches are 7067 and 8241.7 inches respectively. When these are added together and then divided by 518.4, the number of days in a lunation is obtained, 29.53059. The number 5184 is connected to important numbers such as 108 and 12, being 4 x 12 x 108, as well as being 4 x 1296, and 2 x 2592. There is also a curious link between the earth's polar radius (in miles) and the side of the second pyramid: 3949.903 x 12 / (1000 x 8474.8) = 29.53059.
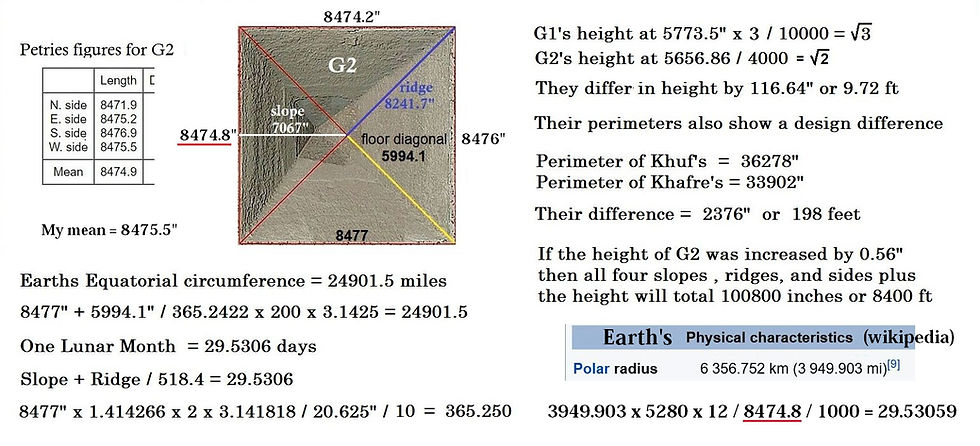
There is also a link to the draconic year, found by Dennis Payne: in English feet, the height of the second pyramid is equivalent to 5 draconic years in days, a number also close to a hundred times the square root of three as noted earlier. The number 1733.1, equivalent to the number of days in 5 draconic years, is also 5656.8384 x 10 / (12 x 2.72).
There are 27.2122 days in a draconic month and a draconic year is 346.62 days, and half a draconic year is 173.31 days. The height of the second pyramid, at 5656.8384 inches, is equivalent to 173.31 Megalithic Yards. So the height of the second pyramid can be said to correspond quite precisely to half a draconic year expressed in Megalithic Yards.
The height of the Great Pyramid is close to expressing the lunar year in Megalithic Yards, but this would give a height which is slightly beyond the error margin (7 inches) given by Flinders Petrie for the height, if using a megalithic yard of 2.72 feet.
Another interesting connection is linked to Venus, found by Jim Wakefield. (6) The sidereal orbital period is 224.701 days. This number multiplied by 12 and pi gives 8,471.0281, close to the mean base side in inches. Venus is relevant to the Moon because the 8 year cycle of Venus is matched to the draconic year of 346.6201 days, via the megalithic yard and the square root of 2, and to 48 lunations, via the royal Egyptian cubit, in the Giza rectangle. We can think of the Megalithic yard as linking the solar year, the 8 year cycle of Venus and the draconic year, as 8 x 10 000 / (346.6201 x 5 x √2) = 32.6401, which is the number of inches in a Megalithic Yard.
1733.1, the number of days in 5 draconic years has connections to both the length and width of the Great Giza Rectangle, which encompasses the outer corners of the three main pyramids at Giza. If we multiply 1 733.1 by 2.72 x 12, giving the height in inches, and then by √2, we get 79.999.7759, which is almost 80 000. There are 8 years in a Venus cycle, which as will see is reflected in the Great Giza Rectangle width, and indeed, if we multiply 80 000 by 365.242199 / 1000, the result is very close to this rectangle's width in inches. If, however, we calculate the height of the second pyramid starting with the 10 000 / √3 inches, as per the diagram below, the height obtained, multiplied by √2, is just over 8000, and then this is a little too big to multiply by the number of days in a year and obtain the Great Giza Rectangle width, approximately. The length of this rectangle is 35 713.2 inches, and this is close to 1 733.1 x 20 x 365.242199 /354.36708 = 35 725.737 inches. The 354.36708 is the number of days in 12 lunations, or a lunar year. So multiplying the height of the second pyramid by the square root of two allows us to access this connection to the draconic year and Venus cycles, together with the ratio between the solar and lunar years, and to do so geometrically to a very high level of precision. And it creates a clear link, astronomical and geometric, between the dimensions of the two largest pyramids at Giza and the dimensions of the Great Giza Rectangle.


The link between the heights of the largest two pyramids incorporates the Metonic cycle of 223 lunar months, and the lunar number 47.
The Metonic period is linked to the Saros period in the side of the second pyramid, as below.



The base side of the second pyramid is also compatible with 2000 x 1.6180339887³ = 8472.13595 inches.
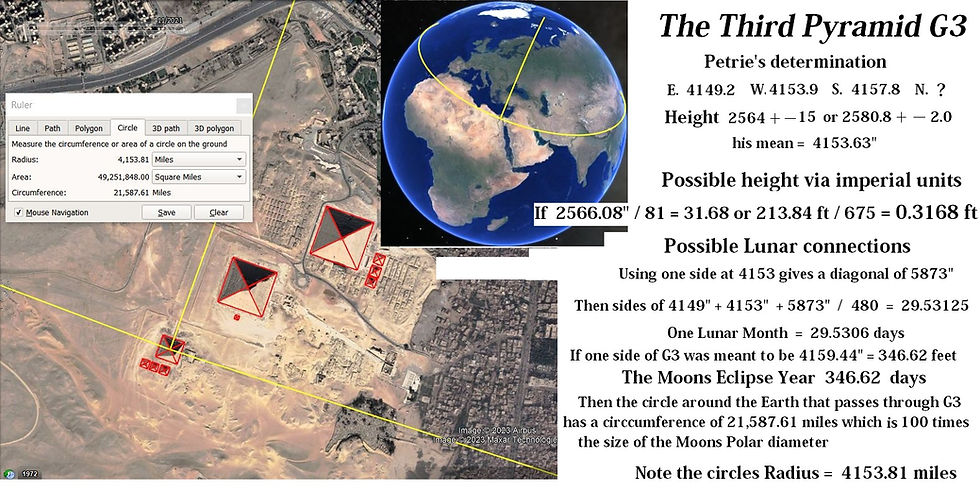
3. The Third Pyramid
Mean base side third pyramid 4,153.6
Height third pyramid 2564 ± 15; or 2580.8 ± 2.0
Side of the third pyramid in inches:
20.625 x 20.618181818 x 29.53059 x 180 /(12.368266 x 44) = 4153.62666. The 20.625 inches and 20.6181818 inches represent two values for the Egyptian royal cubit, equivalent to 0.523875 and 0.523702 m respectively. When we multiply these two values in inches, it is almost equivalent to 29.53059 x 144 / 10.
20.625 x 20.6181818 = 425.25
29.53059 x 144 / 10 = 425.240496
Or we can say 20.625 x 20.618181818 = 354.375 x 6/5 or 354.375 x 12/10.
354.675 is close to a lunar year in days. So the side of the third pyramid can be thought of as 354.36708 x 6 / 5 x 29.53059 x 180 /(12.368266 x 44) = 4 153.5338. And as 12.368266 is approximately equal to 100 π x √3 / 44, then we can say the base is compatible with 2592 x 29.53059² / (100 π x √3) = 4154.0215
The side can also be interpreted as 29.53059² x 25920 / (12.368266 x 440) = 4153.5338
The side in inches can also be interpreted as 29.53059² x 25920 / (1000 x √3 x π ) = 4154.0215 inches.


Looking at the two images above, in which two different ways of approximating the side of the third pyramid in inches are suggested, we can then go on to say that 25920, the canonical number associated with precession, is close to 223 / 235 x 10¹¹ / 254³ x π³ x √3 / 12 = 25 915.81376.
The side can also be equated to 365.242199 x 346.62 x 29.53059 x 9 x 432 / (354.36708 x π² x 1 000) = 4153.0769 inches.
or 365.242199 x 346.62 x 29.53059 x 223 / (354.36708 x 18.02 x 10 x π) = 4155.7893 inches. The 223 is the number of lunations in a Saros period, corresponding to 18.02 years. A saros period of 223 lunations is approximately equivalent to 9 x 18.02 x 29.53059 x 432 / (100π) days.
Or 2 000 x 1.6180339887³ x 30 000 / 254² x 235 / 223 = 4151.5449
Or 20 x 1.6180339887³ x 49 = 4 151.3466
Height of the third pyramid in inches:
20.625 x 20.618181818 x 29.53059 x 180 /(12.368266 x 44 x 1.61803) = 2567.13638
or 29.53059² x 25920 / (12.368266 x 440 x 1.61803) = 2567.0314
or 29.53059² x 864 x √3 / (100 π x 1.61803) = 2567.3328
or 94 sidereal months in days, 94 x 27.32166 = 2568.23604, with 94 being 2 x 47.
The third pyramid side also shows interesting connections to the Great Giza Rectangle, as the two diagrams below show.


Dennis Payne has found that by adding two sides and the base diagonal, the result is 480 x 29.53125. This number of lunar months is also found in the Great Giza Rectangle width, in cubits. A side of the pyramid is also close to 346.62 feet, with this number being the number of days in an eclipse or draconic year.
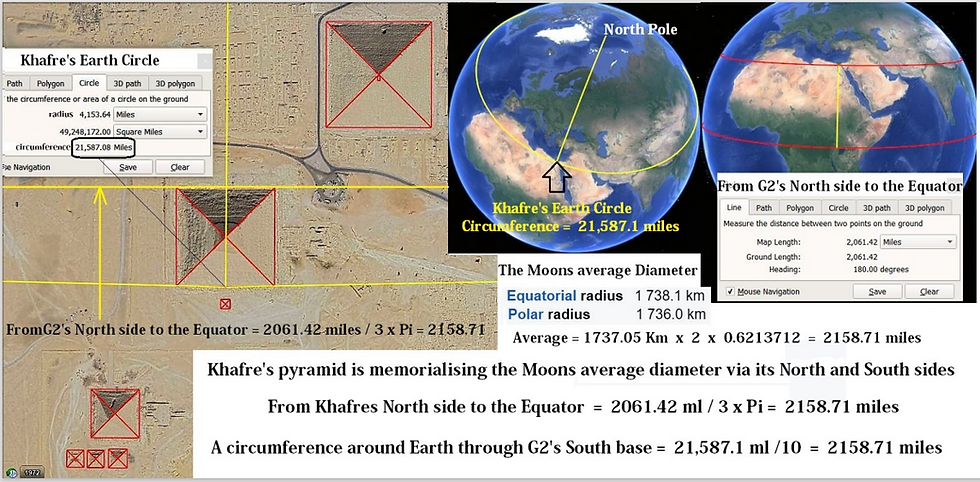
Dennis Payne has also made a connection between the length of a circle of latitude going through the third pyramid, and the polar diameter of the moon.
4. The Giza layout: Rectangles
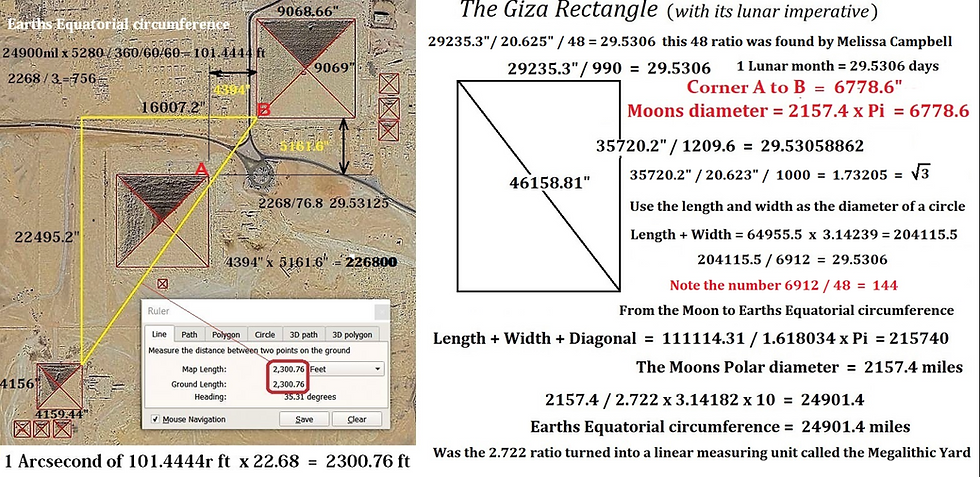
Great Giza Rectangle
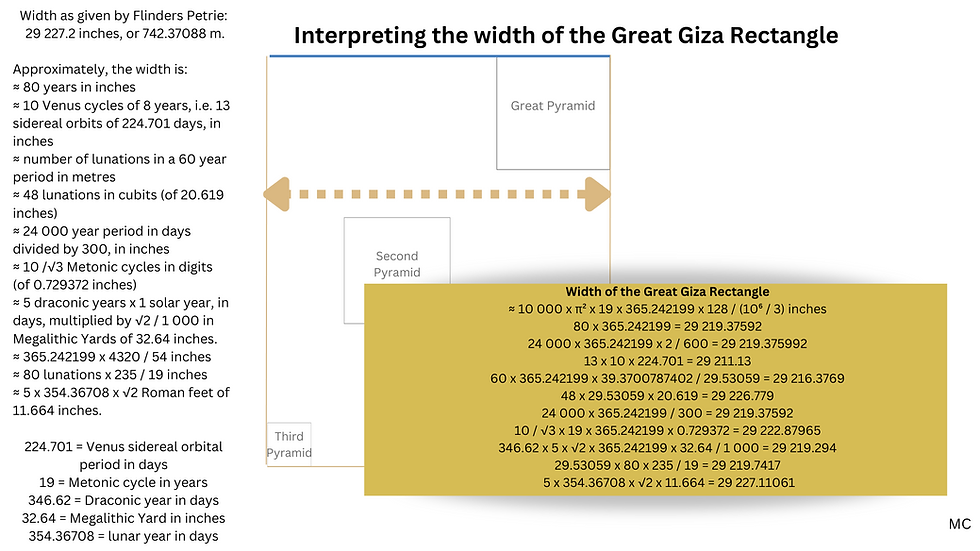
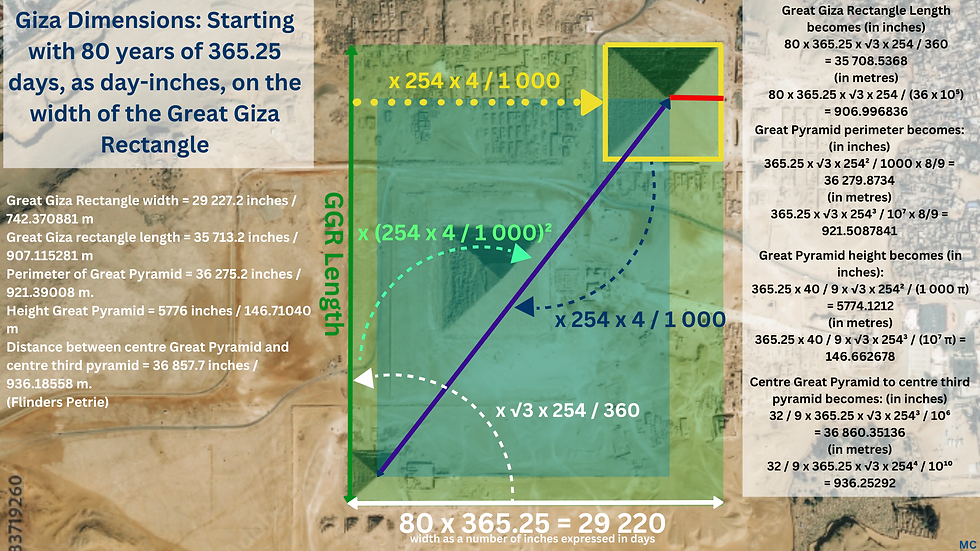
If the three largest pyramids at Giza are considered within a rectangle defined by their relative positions, the dimensions of this rectangle reveal lunar numbers. This rectangle is positioned in line with the north-south axis. Flinders Petrie gives 29,227.19982 inch (W-E) and 35,713.2 inch (N-S) as its dimensions. This could be interpreted as follows:
The west-east width is 29 227.2 inches. There is an ancient cycle of 2922 days according to Cleostratus of Tenedos. an eight-year intercalation cycle, called the octaeteris, to keep Greek civil calendars (which were lunar in nature) in line with the solar year. After 8 years, the moon's phase occurs on the same day of the year plus one or two days. According to 18th century astronomer Jean-Sylvain Bailly, Cleostratus noticed, in 6th century B.C. Greece, that the sun's revolution exceeded 12 revolutions of the moon by 11 ¹/⁴ days. This implies a lunation period of 29.5 days and a solar year of 365.25 days, and 8 such years make 2 922 days. As 11 ¹/⁴ multiplied by 8 is 90, it is equivalent to 3 lunar months of 30 days. So this period of 8 years, or 2922 days came about as a way to reconcile with 96 lunar months, alternating months of 29 and 30 days, with three extra months of 30 days. Two octaeteris is a tetraeteris, and half is the olympic period, which the Greeks were fond of as they held their games every four years, as we do now.
With Flinders Petrie's measure as 29 227.2 inches for the width, this is very close to being 80 x 365.272199 days, and also 80 x 365.259636 days, the mean tropical year and the anomalistic year respectively. It's even closer if we use the coefficient 1.0002766 to multiply the number of days by, on the assumption that an inch related to ours by this number was used at Giza. As a cycle designed to reconcile the patterns of the sun and moon, 80 years is very good, as 80 x 365.242199 / 990 = 29.51452, though not as exact as the Metonic cycle, as 19 x 365.242199 / 235 = 29.53022.
There may be another reason however why astronomers and calendar makers might be interested in an 8 or 80 year period, as it coincides with a cycle of Venus. From our perspective on earth, Venus returns to the same place in our sky on about the same date of the year every 8 years. This happens because 13 Venusian orbits (13 x 224.8 days) very nearly equals eight Earth years. So, to a surprising level of accuracy: 80 solar years are 10 Venus cycles, which are 990 lunations. The Great Giza Rectangle width therefore can be interpreted as encoding the lunar, solar and venusian cycles, in inches.
The west-east width can also be seen as being 29.53059 x12 x 4 x 20.619 = 29226.8 inch, encoding 4 lunar years in cubits of 20.619 inches. We've seen the width is compatible with 80 solar years, providing a link to the sun and Venus, and to 989.461298 lunations in inches, 990 lunations in inches are 48 lunations in Egyptian royal cubits of 20.625, as 990 / 48 = 20.625.
Yet another cycle can be joined to this width: a 600 year cycle known to the Chaldeans and other ancient cultures. In this cycle, the cycles of the moon and sun are reconciled, as with the Metonic cycle. 600 years of 365.242199 days are 7 420.9597 lunations. If a metre is taken as 29.53059 x 4/3 inches, then the width of the Great Giza Rectangle is equivalent to close to 7 420.9597 /10 such metres. 600 x 365.242199/29.53059 x 29.53059 x 4/30 = 29 219.3759. If we multiply this by 1.0002766 we get 29 227.458 inches, equivalent to 742.3774 modern metres.
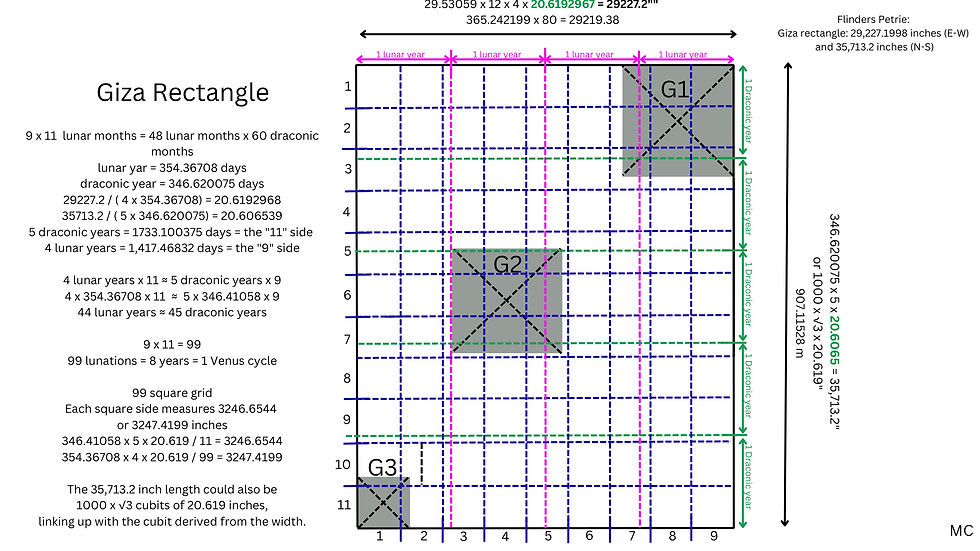
Flinders Petrie has the measure of the north-south span of the Giza rectangle as 35 713.2 inches, but he says: "On the whole, considering the various values of the data, – 5' 40" ± 10" may be taken as a safe statement of the suggested place of the pole, at the epoch of the Pyramid builders." (12) For him, the site is orientated to a point diverging from true north by this amount, and this is the orientation he has used to measure the north-south span.
The north-south length of the rectangle can be understood as 1000 x √3 cubits of 20.61903 = 35 713.2, which were found in the width, resulting from dividing it by 48 and 29.53059. This means that, to within less than an inch, the ratio between the width and length of this rectangle is 48 x 29.53059 / (1000 x √3)
The length can also be understood in terms of 5 draconic years in cubits. A draconic year is 346.620 days, but the cubit here would be shorter, at around 20.6065 inches. 5 draconic years are 1733.10038 days, which is very close to √3x1000, and 4 lunar years in days are reasonably close to √2x1000 days, and this reflects the John Legon view that this rectangle has sides of √2 x √3. The length is also close to 346.62 x 365.242199 x 100 / 354.36708 = 35 725.737, which is draconic year multiplied by solar year multiplied by 100 and divided by lunar year, expressed in inches. In a similar way, the width is also equivalent to 5 draconic years multiplied by a solar year multiplied by √2 and divided by 1000, expressed in Megalithic Yards of 32.64 inches. 5 x 346.62 x 365.242199 x √2 / 100 = 895.19896 MY. A little too long, but close, is 365.242199 x 100 x 346.62 / 354.36708 = 35 725.737, for the length in inches.
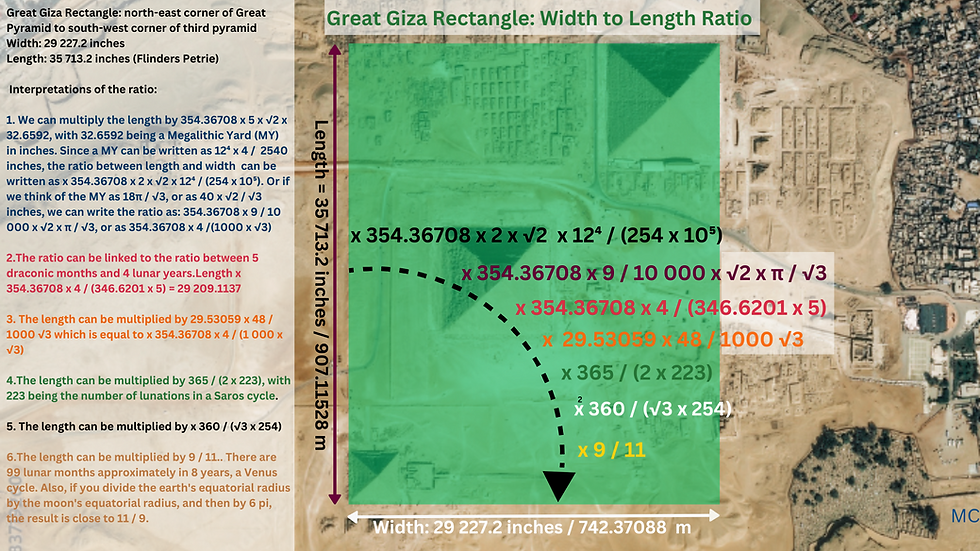
What is the ratio between width and length? 35713.2 / 29227.199 = 1.2219166. There are five possible interpretations here, all with a lunar connection. This is close to 1 / (354.36708 x 5 x √2 x 32.6592), with 32.6592 being a Megalithic Yard in inches. Or 346.6201 x 5 / (354.36708 x 4), the ratio between 5 draconic months and 4 lunar years. It's also close to 1000 √3 / (29.53059 x 48), and to 11 / 9. The lunar connection to the last and simplest ratio is that there are 99 lunar months approximately in 8 years, a Venus cycle. Also if you divide the earth's equatorial radius by the moon's equatorial radius, and then by 6 pi, the result is close to 11 / 9. And the width is also equivalent to the length multiplied by 365 / (2 x 223), with 223 being the number of lunations in a Saros cycle.
Another interpretation is the length is multiplied by 29.53059 x 48 / (1000 x √3) to produce the width. Here, the square root of 3 is kept but the square root of 2 is dropped, in favour of the 48 lunar month connection we find, in cubits, in the width of the Great Giza Rectangle. Another way of thinking of the ratio between width and length is to multiply the length by 29.53059 x 48 / (1000 x √3), which is even more accurate. Another link to the moon is between the length of this Greater Giza rectangle and the Great Pyramid mean base side, which is 9068.8 inches according to Flinders Petrie. This base side multiplied by the number of days in a lunation, 29.53059, and then by 4/30, gives the Greater Giza Rectangle length. It's worth noting in passing that a lunation in days multiplied by 4/3 gives something close to a metre, expressed in inches: 39.37412. Expressing the lunation as 29.53125 days then gives an ancient metre of 39.375 inches.
The Great Giza Rectangle width, there could be a connection to the 24 000 year period associated with precession with the Brahmins and Chaldeans. Le Gentil writes about how the 600 year period in which the sun and moon cycles coincide fits within the greater 24 000 period. If we divided 24 000 years by 600, we get half the width in inches. So, 24 000 × 365.242199 ÷ 300 = 29 219.37592.
The Great Giza Pyramid has a width that is also compatible with 360 / 254 x 365.242199 / 354.36708 x 20 000 x 1.0002766 = 29 224.4582 inches. This is interesting in that if you wanted to divide a circle into 254 parts, perhaps to create a mechanism to monitor the number of sidereal months in a cycle of 19 years, you would have to divide 360 by 254.
The perimeter of the Great Giza Rectangle is very close to being 1000 x √3 x 29.53059 x 7420.9597 / (8 x 365.242199) or 1000 x √3 x 600/8, though this creates a width and length that are slightly too long. Still it is interesting to see the Venus cycle of 8 years combined with the Chaldean period of 600 years. 7420.9597 is the number of lunations in a period of 600 years. The Great Giza Rectangle perimeter is also close to 3600 x 11/9 x 29.53059 inches. The diagonal of this rectangle, as √(29227² + 35723.2²) = 46 155.9989 inches, which is 7 x 223 x 29.53059, with reference to the 223 lunations in a Saros period (Halley).
As with the heights and sides of the three main pyramids at Giza, the length and width of this rectangle can also be related to the number of lunations per year, in inches.
If we go back to the Great Pyramid height, to get to the Great Giza Rectangle we can do so by multiplying by 2π x 29.53059² x 48 / (30 x 1000 x √3), or a more simplified form, we can also multiply by π² x 19 x 365.242199 x 128 / (10⁶ x √3). In this way the width of the Great Giza Rectangle can be defined as 10 000 x π² x 19 x 365.242199 x 128 / (10⁶ / 3) inches. The 24 000 year period is thus approximately π² x 19 x 128 years also. The 80 year period is then 2 x 19 / 300 x (8 x π)² years.
The Great Giza Rectangle width can therefore be related to the 24 000 year period divided by 300, in days, and inches, and to a period of 48 lunar months expressed in cubits, also to 80 solar years expressed in inches, which is also 10 Venus cycles, and also to the number of lunations in the Chaldean 60 year period, expressed in metres. We can also relate this rectangle width to the Metonic period in days, 6939.6018, multiplied by 2 x (8 x π /(10 x √3)² , as 80 is approximately equivalent to 19 x 2 x (8 x π /(10 x √3)².
As a measure in inches, (π x 8)² x 2 / (1000 x √3) = 0.729372, which is very close to the length of a digit, usually given 0.729, 0.729166667, or 0.73333 inches. So the Giza Rectangle width can be thought of as connected to the Metonic cycle in days expressed in digits, (so 365.242199 x 19 x 10 / √3 such digits.
Five draconic years give another interesting link: if we multiply this period, in days, by a solar year, in days, and the square root of 2, all divided by 1000, this gives a number of megalithic yards (32.64 inches or 0.82215 m) which fits within the width of the Great Rectangle of Giza. And this also gives a link w-ith the second pyramid, whose height is 5.664 ± 13 inches according to Flinders Petrie. This height is equivalent to half a draconic year expressed in megalithic yards. The width of this large rectangle is therefore equivalent to the height of the second pyramid multiplied by the square root of 2, which gives almost exactly 8,000, which reminds us of the Venus cycle, then 365.242199 / 1,000.
Another interpretation of the width is as 29.53059 x 4 x 4700 / 19 = 29 219.7417 inches (which becomes 29 227.8239 inches when multiplied by 1.0002766). This refers to the Metonic cycle, as 4700 lunations of 29.53059 days are 380 years of 365.24677 days. This seems to be a way of merging the numbers linked to 80 solar years, with its lunar and Venus connections, and the Metonic cycle of 19 years. So 80 years are equivalent to 4 x 4700 / 19 lunations, and this width is 80 lunations multiplied by the Metonic coefficient 235 / 19, in inches. This connection is reflected in the width being linked to the length by 365 / (2 x 223), with 223 being the number of lunations in a Metonic cycle of 19 years. So in this respect the rectangle is Metonic.
The width can also be thought of as 9² x 12² x 5 x 354.36708 x √2 / 1000 = 29 227.11061 inches. As 9² x 12² = 11 664, and a Roman foot is 11.664 inches, it can be interpreted as 5 x 354.36708 x √2 Roman feet.
The reason why various parts of the Giza Plateau appear to be connected by these figures could be a need to represent various celestial harmonies.
Not directly moon related, but of interest, is that the equatorial circumference of the earth, 24,901.461 miles, is 54 000 times greater than the Great Giza Rectangle width. 29 227.2 x 54 000, if the width is read as 29 217.714 inches. There is an indirect lunar connection in fact, as the equatorial circumference of the earth divided by the equatorial circumference of the moon is approximately 11 / 3, and the ratio of this rectangle is 11 x 9. The equatorial circumference of the moon is 6 785.8401 miles. 54 is twice 108, and the equatorial radius of the moon is 1 080 miles. 24 901.461 / 6 785.8401 = 11.0089 / 3
The two diagrams below suggest that a simple geometric construction based on a length of 29.53059 inches can account for the width and length of the Great Giza Rectangle design. the geometric values are then multiplied by a coefficient of 1.0001415 to match the measures on the ground better. This figure is simply ((29 227.2 / 29 222.8685) + (35713.2 / 35708.3769)) / 2. This is close to the other coefficient used elsewhere of 1.0002766, which could be used instead. Both of these coefficients are used in an attempt to bring the values up to the dimensions given by Flinders Petrie, on the assumption that our modern inch,and Flinders Petrie's inch, are very slightly bigger than a hypothetical inch used at Giza.
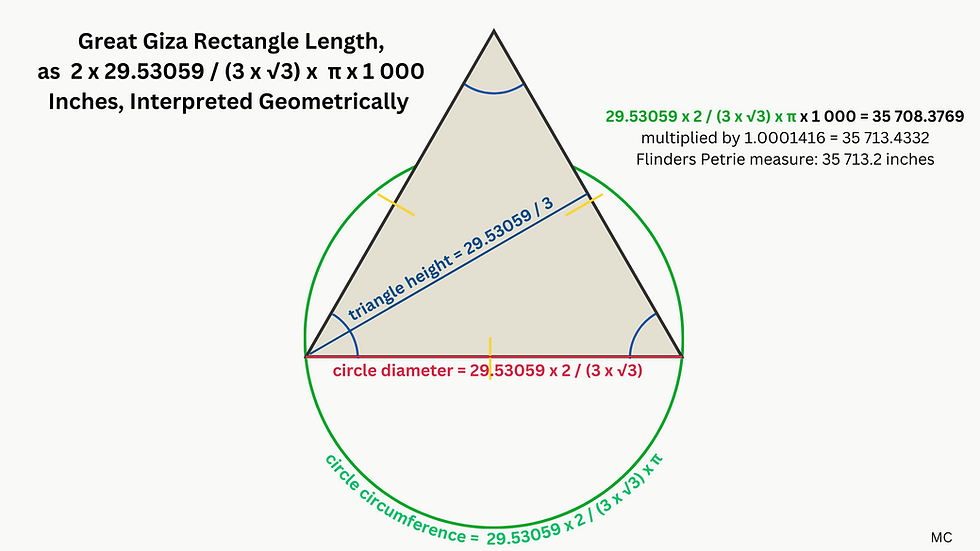
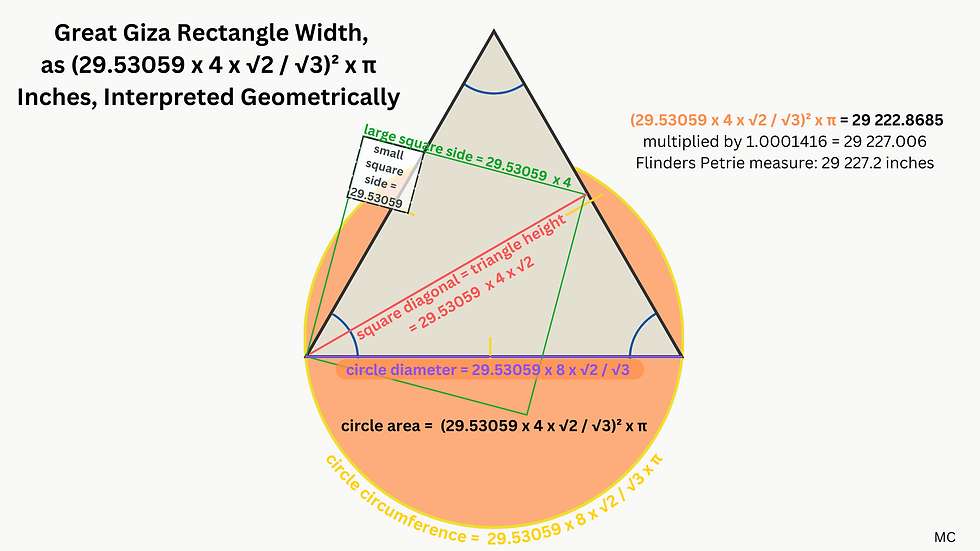
The significance of the square root of three and pi is probably due to the fact that the main solar and lunar cycles can be grouped into an equation, which is approximately equal to π /√3. It's possible that this equation is at the centre of the system which the pyramid complex represents, with the cycles measured out in days, represented as inches.
365,242199 x 346,62 x 3/ (354,36708 x 29,53059 x 20) = 1,81468
π /√3 = 1,8138



Of these options, the two ratios that match the width and length of the Great Giza Rectangle most closely are: length x 354.36708 x 4 /(1000 x √3) and length x 365 / (2 x 223). However, they are all quite close matches, and they can perhaps all be considered possibilities.
There is also a lunar quality to the perimeter of the Great Giza Rectangle:

Metonic Giza Rectangle
The Metonic rectangle offers another lunar dimension to interpreting the Giza design, which does not rely on any unit, but only on proportion. It raises questions on the use of geometry to express the Metonic cycle not just with a circle, but also with a rectangle. Looking into the Great Pyramid base as part of a circle also raises questions on the use of the day-inch at Giza. Flinders Petrie gave the length of the distance between the centres of the Great Pyramid and the third pyramid as 36857.7 inches, which is 936.18558 m. If this line is the diagonal of a rectangle, the length, north-south, is 29102 inches, or 739.1908 m, and the width, west-east, is 22616 inches, or 574.4464 m. If we take the width and multiply it by 29.53059, the number of days in a lunation, and 38, we get the length. And conversely, if we multiply the length by 365.242199, the number of days in a year, and divide by 470, we get the width again. It's a Metonic rectangle.
The number 47, combined with the number 38, is present in this Giza rectangle, which stretches out between the centres of the Great and third pyramid at Giza. A lunation of 29.53059 days, multiplied by 47 x 10, and divided by 19 and 2, gives the solar year, approximately, as 365.24677. This means the number of lunar months on average per year can be simplified as 470/38, which is 12.36842 and 365.242199 / 29.53059 = 12.368266. This solar and lunar ratio is slightly different to the one found at the Rollrights by Jim Wakefield, yet it also uses the number 47. At the Rollrights, the radius of a circle was 47 Saxon feet, and the circumference was approximately 10 lunar months in days expressed as Saxon feet. At Giza, we have a rectangle, and the ratio between the width and length is 38 / 29.53059, to within about half an inch: which is roughly equal to 365.242199 / 470. The width of 22616 x 38 / 29.53059 = 29 102.29697. The length as given by Flinders Petrie is 29102. This 29102 multiplied by by 365.242199 / 470 = 22 615.47379, which is 0.5262 inches less than Flinders Petrie's figure.
The 22 616 inch side is approximately equivalent to 7200π inches, or to 1900 x 29.53059 x π x 2 / (√3 x 9). This is especially interesting as a lunation in days multiplied by 4/3 is, in inches, approximately a metre, and when this is multiplied by pi and divided by 6, you would expect to obtain a cubit. So here we have 29.53059 x 4/3, a metre, x π/6, a cubit, and then x 1900 / √3, the width of this rectangle. And as elsewhere, the π / √3 theme returns here too.
The diagonal of this Metonic rectangle might be of interest also. The diagonal is 36857.7 inches, as per Flinders Petrie, which is close to the perimeter of the Great Pyramid x 4 x 254 / 1 000, so 9 068.8 x 4 x 4 x 254 / 1000 = 36 855.6032, two inches under Flinders Petrie's measure. 254 is the link between a metre and an inch, as 2.54 cm are an inch, and it's also a link between the solar year and lunation, as 29.53059 x π x 1 000 / 365.242199 = 254.0042898. The diagonal equivalent to the perimeter of the Great Pyramid as it expressed in metres, 921.39, but as a value expressed in inches, multiplied by 40. So we can interpret the diagonal as √2 / √3 x 16 000 000 / 354.36708 = 36865.5725 inches, though this is perhaps a little too long, or else as π / √3 x 254 x 80 = 36 856.40308 inches, which is very close to 36 857.7. Or more simply in metres, π / √3 x 8 / 1000 x 254² = 936.152638.
As a result, the Great Pyramid base perimeter of 9068.8 x 4 inches multiplied by 354.36708 x π and divided by 3 and 365.242199 is 36 856.2254 inches, just over an inch under the Metonic rectangle diagonal as measured by Flinders Petrie. Another way of expressing this is 2000 π / (3 x √3) x 354.36708 / 365.242199 = 36 857.0252 inches.
In a similar way, the base side of the Great Pyramid can be expressed in inches as 5000 π / √3, the second pyramid base side as 14 000 π / (3 x √3), and the third pyramid base side as 29.53059² x 864 x √3 / 100 π. So this diagonal fits in with the use of pi and the square root of three elsewhere.
Another way of interpreting the diagonal is 6 x 6 x 7 x 8 x 8 x 9 x 254 / 1 000 = 36 868.608. And if we divide this by the coefficient 1.0002766, the result is 36 858.41296, which is very close to 36 857.7 inches.
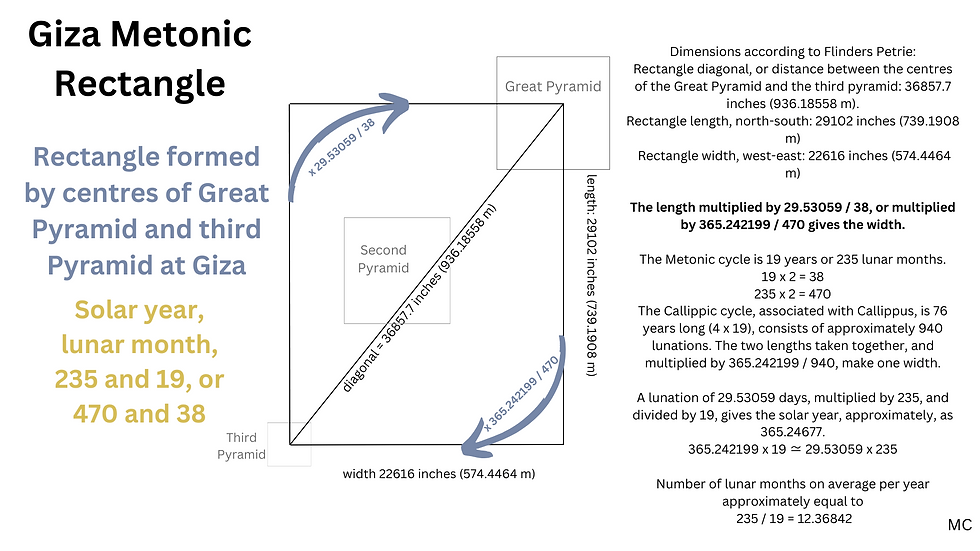
To summarise, the rectangle formed by the centres of G1 and G3 is that it is Metonic in character, both in measurement and in proportion. The width given by Flinders Petrie is 22 616 inches, which can be interpreted as 1900 x 29.53059 x 2π/(3 x √3) x 1/3 = 22 616.3054 inches. And length x 365.242199 / 470 gives width. The length is 29102 inches. So to get from length to width: 365.242199 /470 x 29 102 = 22 615.4861. 19 is the number of years in a Metonic cycle, 29.53059 is the number of days in a lunation, 470 is twice 235, the number of lunations in a Metonic cycle, and π / (3 x √3), for me, symbolises the system of time keeping, because: civil year x draconic year / (lunar year x lunation) ≈ 20π /(√3 x 3), with civil year: 365 days, draconic year: 346.6201 days, and lunar year: 354.36708 days. Also: number of lunations per year ≈ π /√3 x 300 / 44.
Below we can see that two lunar rectangles can be seen to define the space at Giza, and they are lunar not by virtue of any particular unit of measure, but in their proportions.


5. The Giza Layout: Distances between Pyramids
Dennis Payne has also found that if we take the measure between the third pyramid and the Great pyramid, centre to centre, we obtain a measure of 36 864 inches. Using a measure of 9071.8 inches for the side of the Great Pyramid, we can divide this by 36 864, and then multiply by 120, which gives 29.5306.
Combining Pyramid base sides
Mean side of the Great pyramid, 9068.8 inches, multiplied by a mean side of the third pyramid, 4153.6 inches, is equivalent to 3,000 x 29.53059 square cubits, each measuring 20.62 inches. As Dennis Payne has suggested this can be further refined to 201.434 x 439.806 / 29.5306 = 3000.003.
The image below shows possible lunar interpretations of the dimensions of the rectangle formed by the positioning of the three pyramids. One side of the Great Pyramid multiplied by one side of the third pyramid, in cubits, produces 3000 lunar months. (439.821 x 201.442) = 29.53059 x 3000.225.
The relative layout of the two largest pyramids. The N-S distance between their south faces is 346.32 metres, and the N-S distance between their centres is 353.68 metres.
The distance between the centres of the Great Pyramid and the third Pyramid (ground measure) is 36 857.7 inches. As Dennis Payne has found, if this length is the side of an equilateral triangle (as per the diagram below), and then halved to produce the yellow triangle, the perimeter of the triangle will be 29.53059² x 100 inches.
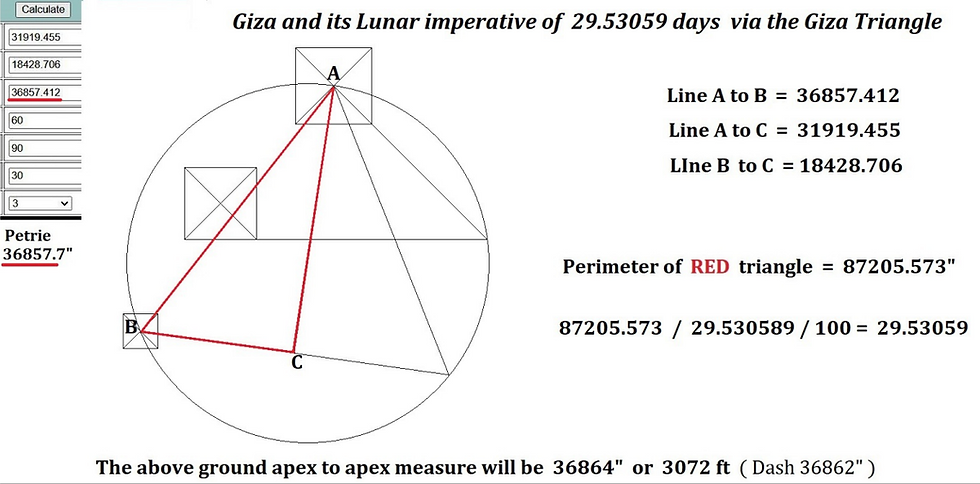

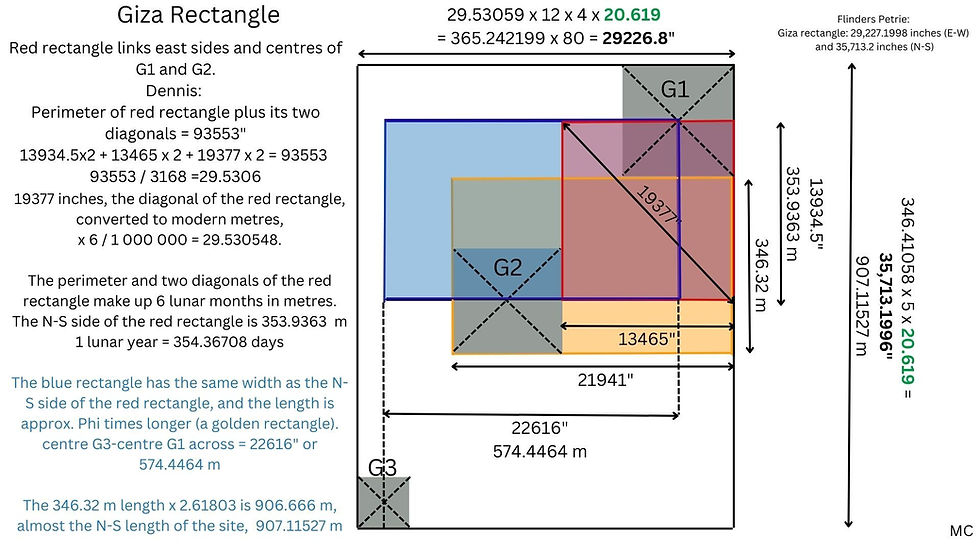

If a rectangle is drawn, as per the diagram below, by Dennis Payne, the number 29.53059 appears in the diagonal of 19377 inches. Converted to modern meters, multiplied by 6 and divided by 100, this gives 29.530548 m. Thus the perimeter and the two diagonals of the red rectangle constitute 6 lunar months in metres. The number 254 relates the metrr to the inch. However, the diagonal can also be interpreted as solar, in that it is 365.242199 x 1000 / 6π = 19 376.7 inches.
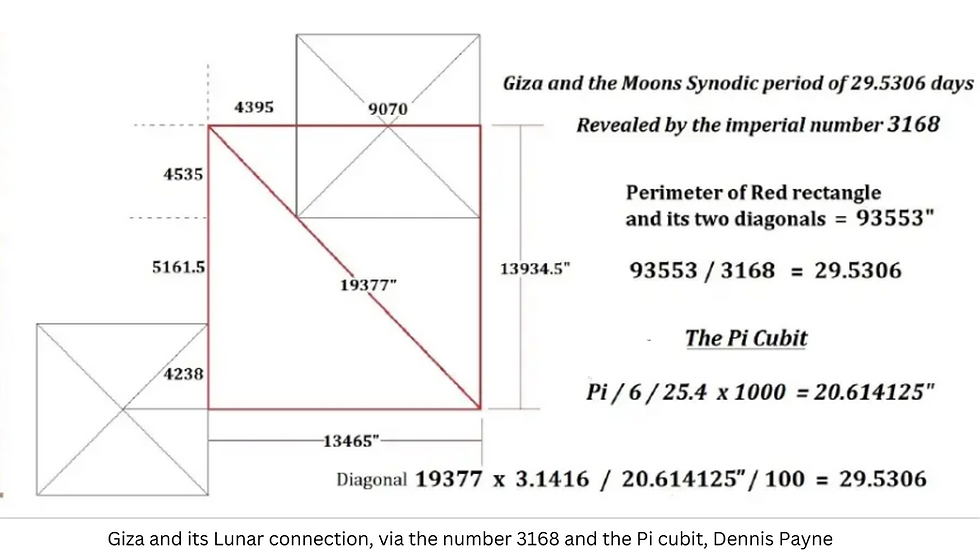
Analysing the proportions of some of the other rectangles created by the pyramids can lead to interesting results.
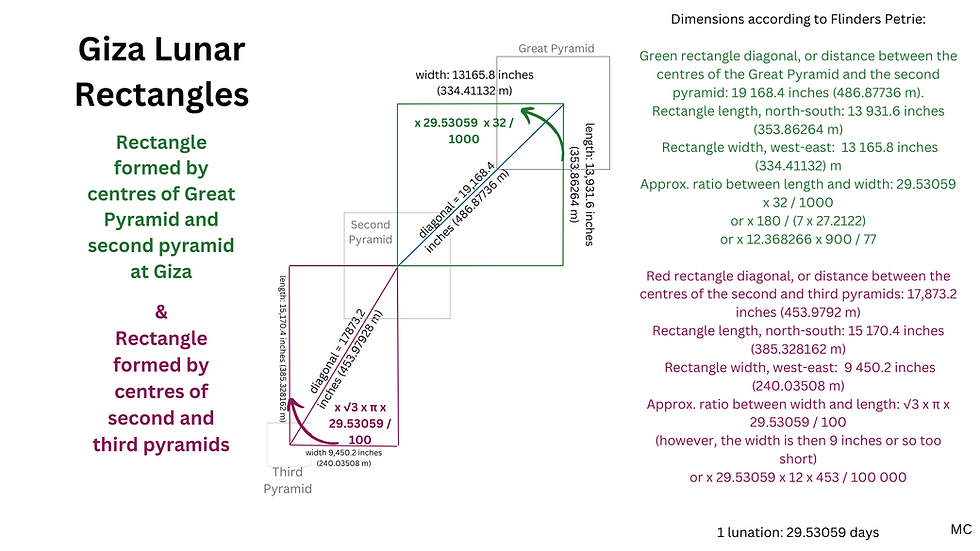
6. General lunar connections at Giza
Dennis Payne has found that the moon's size is encoded in a length at Giza: the distance from the north west corner of the Great Pyramid to the south west corner of the third pyramid is 3417.5 feet, which, multiplied by 10 000 / 3 and divided by 5280 to convert to miles gives 2157.5126, which the moon's polar diameter in miles.

The perimeter around the two largest pyramids also is linked to a lunation in days, according to Dennis Payne:
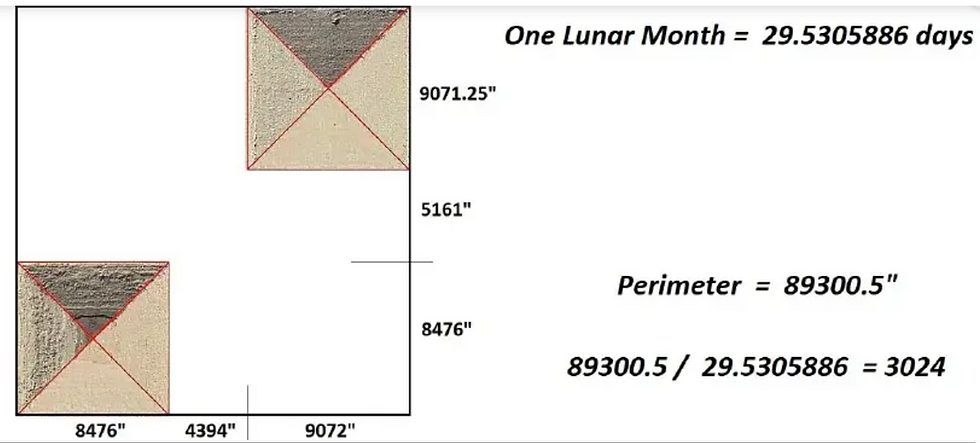
This find of Dennis Payne's shows a link between the dimensions of the three main pyramids, the number of days in a lunation, and the mean circumference of the earth in miles:

The three perimeters plus the six diagonals, divided by 29.53059 and multiplied by pi (here Dennis has used 3.142) gives the average circumference of the earth. The number 24,883.2 is 12⁵ / 10 miles, equivalent to 40,045.6287 km. The equatorial circumference is 24,901.461 miles, or 40,075.017 km, and the polar circumference is 24,859.734 miles, or 40,007.863 km, giving an average of 24 880.5975 miles, or 40,041.44 km. Using calculator pi, 3.14159265... the result is even closer, 40,040.4551 km, about 1 kilometer less than the average circumference.
Jim Wakefield has found that the side of the Great Pyramid is linked to the mean circumference of the moon. If we take this as 2158.7 miles, divide by pi and multiply by the number of inches in a Saxon foot, 13.2, the result is 9070.1893. This is the side of the Great Pyramid in inches. However, here the numbers are what is important, as we are combining miles with Saxon feet in the same calculation.
Dennis Payne has also uncovered a compelling connection between the Giza site and the moon's diameter, as well as to the pi cubit, which is based on a circle with a diameter of 1 metre, the circumference being then divided into 6 equal parts. The circle of latitude which runs through the south side of the second pyramid is 21 587.06 miles long, and the mean diameter of the moon is 2158.7062 miles. As Dennis writes: "The astounding thing about the measure of this circles circumference is that it is 21,587.06 miles in length, or 10 times the Moons average diameter . Clearly one can only come to one conclusion and that is they are memorializing the Moons dimensions via Khafre's pyramids position on Earth." (11)
Furthermore, the mean diameter of the moon, multiplied by 3 and divided by 100 and pi, gives the value in inches of the pi cubit, 20.61425 inches long. Incredibly, the distance from the second pyramid to the equator is 2061.4125 miles.
This cubit also very nearly expresses the ratio between the solar and lunar years multiplied by 20, a ratio which also approximately links the metre and the inch ( 365.25 x 10 / (π x 29.53059) = 39.370255).
This means that the mean diameter of the moon is also equivalent to 352 000 x π² metres. 352 is 3 168 / 9, and also 4 x 88, offering a Mercury connection, as its sidereal orbital period is 87.9 days. There is also a Mars connection, as 365.242199 / (29.53059 x 12) x 2000 / 3 = 687.1259, and the Mars sidereal orbital period 686.980 days. These 686.98 days multiplied by pi give 2158.6697, close to the moon's mean diameter in miles.
Interpreting the distances and proportions in terms of cycles of time
A close examination of the dimensions of the pyramids and their relative position reveals a simple progression from 10 000 inches can explain many of the dimensions, as illustrated by the algorithm diagrams below. The first one, in yellow, starts with the number 10 001.48222, and the second, in pink, starts with 10 001.17441833, two variations on an ideal 10 000 inches, adjusted slightly to fit with Flinders Petrie's measures, and the third starts simply with 10 000. The fourth, in blue, starts by taking inspiration from Richard and Robin Heath's work in Brittany, by taking 366 sidereal months, which make almost exactly 10 000, and then using a coefficient to convert the inch to what might have been the inch used at Giza. This coefficient is 990 x 29.53059, so 990 lunations, divided by 29 227.2, Flinders Petrie's measure for the Great Giza Rectangle width, so 1.0002766.


The number 29.53059, which is the number of days in a lunation, comes up again and again. Why is it used as a factor to multiply things by? By a strange natural coincidence, 29.53059² x 25 x pi / 365.242199 = 18.99999274. And 29.53059 x 25 / pi = 234.99696855. 235 is the number of lunations in a Metonic cycle, and 19 is the number of solar years in such a cycle. Without even looking for it, the Metonic cycle comes up simply by squaring this lunar number, 29.53059, and multiplying it by pi and 25, or by pi and 100 / 4.

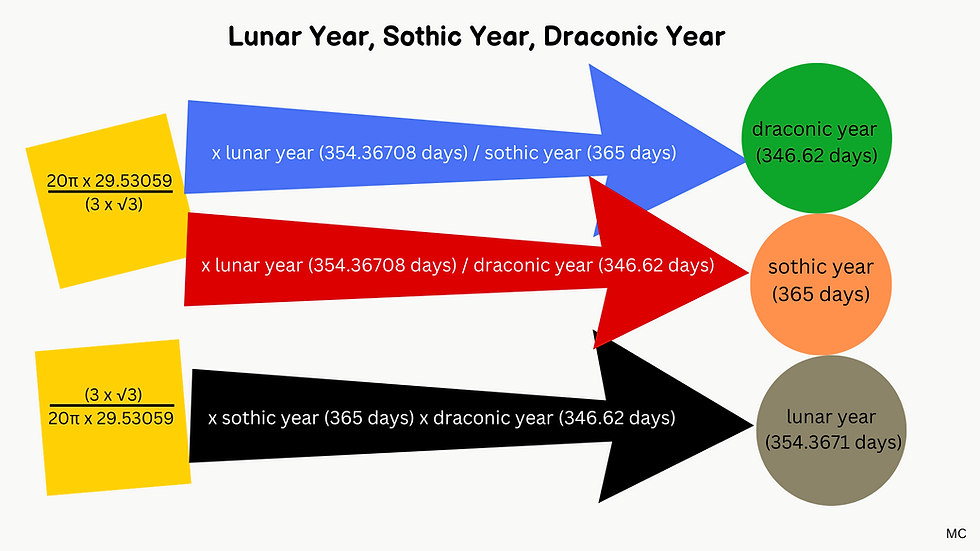
By multiplying the number of days in a Sothic year by the number of days in a Draconic year, and 3√3, then dividing by 20π and the number of days in a lunation, 29.53059, we can obtain approximately the number of days in a lunar year. Perhaps this why we find the square root of 3 and pi in various proportions at Giza.
If we take the period of a Sothic year as 365.25 days, and a draconic year as 346.6201 days, multiply them by 3√3, and divide by 20π and 29.53059, this last number being the average number of days in a lunation, and π being the ratio between a circle's circumference and diameter, we get 354.54703, which is very nearly the average number of days in a lunar year (about 4 hours and 19 minutes short). In the same way, we can obtain the approximate value of the Sothic year as 20π x 29.53059 / 3√3 x the number of days in a lunar year, divided by the number of days in a draconic year. And by the same token, the draconic year is the lunar year divided by the sothic year multiplied by 20π x 29.53059 / 3√3. So it's interesting that the height of the Great Pyramid is close to 10 004 / √3 inches, x 2π gives the pyramid perimeter, x 29.53059 / 30 gives the Great Giza Rectangle length, which multiplied by 300 / 365.242199 gives 24 000, the number of years in a precessional cycle, according to some ancient traditions, including the ancient Indian and Chaldean.
All the main dimensions, the three pyramid heights and base sides, can be related to the number of lunations per year, 12.368266, and a couple of other numbers such as 440, 47, 2, 4, 3, 6, 9 and pi, and the square root of 3. The mean number of lunations can be interpreted geometrically as 1000 x √3 x π / 440. See below.

The dimensions at Giza tell that irrational numbers can be used to express time cycles:
5 draconic years of 346.62 days are close to 1000 √3 days.
A lunation can be expressed as 125 x 365 x √3 / (223 x 12) days
The mean number of lunations per year is close to π x √3 x 100 / 44
A Saros period (Halley) of 223 lunations can be expressed as 125 x 365 x √3 / 12 days.
A draconic month is 125 x 365 x √3 / (242 x 12) days
A draconic year of 346.62 days is close to 80π x 29.53059² / (√3 x 365) days.
A factor of 20π x 29.53059 / (3 x √3) links the sothic, draconic and lunar years. This is also close to 28 / 10 000. Let's call 20π x 29.53059 / (3 x √3) 'LF' (lunar factor).
LF x lunar year (354.36708 days) / draconic year (346.62 days) approximates the sothic year (365 days).
LF x lunar year (354.36708 days) / sothic year (365 days) approximates the draconic year (346.62 days).
1/LF x sothic year (365 days) x draconic year (346.62 days) approximates the lunar year (354.36708 days).
The length of the Great Giza Rectangle is close to 100 times LF in inches, so 2000π x 29.53059 / (3 x √3) inches. (When multiplied by 1.0002766 it is closer still)
If we divide this factor LF by 29.53059, we get 2000π / (3 x √3), and this links many parts of the Giza site. Let's call 2000π / (3 x √3) 'F'. Multiplied by 30, F gives the Great Pyramid perimeter, and the perimeter divided by 2π gives the Great Pyramid height. Multiplied by 223 x 29.53059 / (47 x 20) , F gives the second pyramid base side in inches, and F multiplied by 223 x 29.53059 x π / (47² x 2) gives the second pyramid height in inches. Multiplied by 29.53059, F gives the Great Giza Rectangle length in inches, and the width is obtained by multiplying the length by 9/11, or 29.53059 x 48 / (1000 √3), or 354.36708 x 5 x √2 x 32.6592 / 100 000, or 354.36708 x 4 / (346.6201 x 5). F multiplied by (29.53059 /π )² x 9 x 432 / 100 000 gives the third pyramid base side in inches. And F multiplied by (29.53059 /π ²) x 9 x 432 / (100 000 x 1.61803) gives the third pyramid height in inches. From this we can make connections between the various parts of the Giza site, such as Great Giza Rectangle length multiplied by 9 x 432 x 29.53059 / (π ² x 100 000) gives the third pyramid base side, or the height of the second pyramid is the height of the Great Pyramid multiplied by π³ x 29.53059 x 223 / (365.242199 x 19 x 30), etc.
As well as linking various parts of the Giza site, these factors also link various cycles related to the sun and moon, as well as Venus, as seen from earth. These cycles are expressed in inches mostly, as well as in metres, and cubits, which are units that make sense as astronomical time periods in inches.
The use of irrational numbers, such as pi, Phi, and the square root of 3, links these cycles to geometry. This provides a practical way of mapping on the ground the relations between various time cycles. It also enables us to express something of the divine in these workings, as irrational numbers convey something of the limitations of human mathematical notation in that they cannot be expressed as fractions or decimals accurately.


Visualising these ratios simply is helpful in terms of understanding the dimensions in inches of various parts of the site.
For example, the side of the second pyramid can be understood as simply 223 x 38 = 8 474 inches, 223 being the number of lunations in a Saros period (Halley) and 38 being related to the Metonic period, as 365.242199 x 38 / 470 gives approximately the number of days in a lunation.
Or as the diagram above shows, the side of the second pyramid can be interpreted as 100 π x 223 x 29.53059 / (47 x 3 x √3) = 8474.2426 inches.
Or the side of the third pyramid can be understood as 25.92 x 29.53059² / ( π x √3) = 4154.0215 inches, with 25 920 being the traditional value for the number of years in a precessional cycle; or as 7 200 /√3 = 2 400 x √3 = 4156.9219 inches.
Or as 25 920 x 29.53059² / (1 000 π x √3) = 4154.0215 inches. (The astronomical-geometric figures can be multiplied by 1.0002766).
The side of the Great Pyramid can be interpreted as 5000 π / √3 = 9068.9968 inches, or as 346.62 x 365 x 3000 / (4 x 354.36708 x 29.53059) = 9067.3891 inches, bringing together the number of days in a sothic year, draconic year, lunar year, and a lunation.
If we multiply the sides of the three pyramids, with the astronomical and geometric values, from the diagram above, 8471.2426 x 4154.0215 x 9068.9968, this is approximately equivalent to:
Great Pyramid 346.62 x 365 x 3000 / (4 x 354.36708 x 29.53059) x second pyramid 100 π x 223 x 29.53059 / (47 x 3 x √3) x third pyramid 25.92 x 29.53059² / ( π x √3), which simplifies to 346.62 x 365 x 18 000 x 223 x 29.53059 / 47.
This is similar to 223 x 29.53059³ x 2 400 x π x √3 x 1 000 / 235,
which is also 20π x 29.53059 / (3 x √3), 'LF' (lunar factor), multiplied by 29.53059² x 223 x 10 800 / 235.
The Great Giza Rectangle length can be interpreted as 880 x 365.242199 / 9 inches, bringing together an orbital period of Mercury and a year, with the number 9, or 2000 x π x 29.53059 / √3 x 3 inches, or 223 x 29.53059 x 220 x 9 /365 inches.
If you wanted to obtain the value in days of a lunation from the height of the third pyramid, for example, you could take Flinders Petrie's measure, 2564 ± 15; or 2580.8 ± 2.0 inches, let's call it 2567.33, you could obtain it as: √(2567.33 x π x Phi x √3 x 1 000 / 25 920), or √(2567.33 x π x (√5+1) x √3 x 1 00 / 5184).
Or to get the value of a draconic year, starting with 2567.33, you could multiply it by π² x Phi x 8000 / (365 x 2592) to get 346.6811, a little over the actual value of 346.62 days.
Or with the height of the third pyramid, with Flinders Petrie's measure of 4,153.6 inches, √(4153.6 x π x √3 x 1 000 / 25 920) = 29.52909, and with a value of 4154.0215 instead, the result is 29.53059.
Another interesting combination is multiplying the base sides of the great and third pyramids, as mentioned earlier. With 9068.9968 and 4151.0215 inches taken as the astronomical values for these two pyramids' sides, √(9068.9968 x 4151.0215 / (3000 x 29.53059) = 20.6139. The result could be interpreted as the values of the two sides expressed in cubits of 20.6139 inches, multiplied together. Or, since the ratio between the solar and lunar years multiplied by 20 is 20.613777, multiplying the side of the Great Pyramid by the side of the third pyramid it could be interpreted as 9068.9968 x 4151.0215 = (365.2446 x 20 / 354.36708)² x 29.53059 x 3000, which simplifies to 365.2446² x 100 000 / 354.36708.
Multiplying the side of the second pyramid by the side of the third, in inches, so with 8474.2426 and 4154.0215 is equivalent to 29.53059³ x 223 x 1 440 / 235, which brings together two cycles, as 223 months corresponds to the Saros cycle (Halley) and 235 months to the Metonic cycle.
Dividing the side of the Great Pyramid by the side of the second pyramid, using 9068.76 and 5662.38, is equal to 365.242199 x 19 x 30 / (2 x π² x 29.53059 x 223). Here again we find the Metonic and Saros cycles of 19 and 18.03 years, mixed with the ratio between the solar year and a lunar month.
Multiplying the side of the Great Pyramid as 9072 inches by 365.242199 / (29.53059 x π) gives the length of the Great Giza Rectangle, as 35715.9325 inches. Or the height of the Great Pyramid as 5775 inches, multiplied by 365.242199 / (29.53059 x 2), gives the Great Giza Rectangle length, as 35 713.3687 inches.
The dimensions at Giza reveal the repeated use of numbers associated with astronomical cycles, though not necessarily in the way you might expect. There isn't a particular stretch that measures a year, or a lunation in day-inches, for example. There doesn't seem to be an indication that one pyramid is about the draconic cycle, and another about the solar / lunar year ratio. Rather, the various numbers that make up the ratios between these cycles are dotted about the site, jumbled up in unexpected ways. This could indicate that it is the system as a whole that was deisnged to take into account various astronomical cycles that is present at Giza.
Some equivalences seem to arise from the number combinations. For example, 365.242199, the number of days in a solar year, is roughly equivalent to 4 x 29.53059² x 27.3166 x 366 x 864 / (275 x 100 000 x 3) = 365.2345, with 27.3166 being a sidereal month in days, 366 being the number of days in a leap year, and 864 / 275 is an approximation of pi. This provides simple ratios to relate these various cycles to each other. So we can multiply two types of lunar month by 366 / 100 000 and pi to approximate the solar year. And we can define one cycle in terms of other cycles, for example, the sidereal month of 27.3166 days is approximately equal to 80 x 365.242199 x 90 000 / (48 x 29.53059² x 2 x pi x 366) = 27.3191. By not simplyfing this, we can see the connection to the Giza rectangle width with 80 solar years and 48 lunations, so that we can multiply this width in inches by 90 000 / (48 x 29.53059² x 2 x π x 366) to approximate a sidereal month. This also harps back to the Great Pyramid, where the height was related to 366 sidereal months, as here 80 x 365.242199 x 90 000 / (48 x 29.53059² x 2 x π) is equal to 366 x 27.31912 = 9998.799, and if this is divided by √3, we get back to the Great Pyramid height in inches.
The sidereal year can also be approximated by the ratio between the solar year and a lunar year, 365.242199 / 354.36708, multiplied by 900 000 / (29.53059 x π x 366) = 27.3191, or as a length in inches, 90 000 / (29.53059 x 2 π x 366) Egyptian royal cubits of 20.613777 inches.
The draconic year of 346.62 days is close to 28 x 365.242199 / 29.53059 = 346.3115. It's also close to the diameter of the sun in inches, as 864 000 x 5280 x 12, divided by 365.242199 and 432 000 = 346.9479.
Also we've seen that pi itself can be approximated in terms of astronomical cycles. Here for example, we can loosely define it as 365.242199 x 3 / (366 x 27.3166 x 29.53059² x 4) = 3.1418846.
It also hints at links to units of measure such as the metre, which is close to 29.53059 x 4/3 = 39.37412 inches, and the Roman foot, compatible with 29.53059² / 100 x 4/3 = 11.6274 inches. We could say that a year can be expressed in in inches as 27.3166 x 366 x 864 / (275 x 100 000) Roman feet of 11.6274 inches, for example. Or even by 10π Roman feet of 11.6274 = 365.2855 inches. Likewise, 29.53059 x 27.3166 x 366 x 864/ (275 x 100 000) metres of 39.375 inches can express a year, as 365.2426 inches, or with the modern metre, 365.1970 inches.
The 3 600 year cycle can be approximated quite well with a draconic month, a synodic month, and pi: (27.2122 x 3 + 1) x 29.53059 x 366 x π x 2 / (900 x √3) = 36 000.0162. Likewise the 600 year cycle is (27.2122 x 3 + 1) x 29.53059 x 366 x π x 2 / (5 400 x √3) = 600.0003. The three synodic months are useful markers in themselves as after that period the moon returns to the same constellation.
Since the height of the Great Pyramid can be interpreted as 366 sidereal months of 27.32166 days, and the side can be interpreted as 7.8 lunations of 29.53059 days in metres, it's possible to approximately link these two types of month accordingly. 29.53059 x 7.8 x 20 000 x √3 / (366 x π x 254) = 27.32075. The number 254 is the conversion between inch and metre, but it's also a link between the solar and lunar cycles. 365.242199 x 254 / (1000 π) = 29.53009. So we can say that a sidereal month of 27.32166 days is approximately equivalent to 156 x 365.242199 x √3 / (366 x π²) = 27.320292. As a result, we can interpret the height of the Great Pyramid as 365.242199 x 156 x √3 / π² = 5773.0564 inches, and the side as 365.242199 x 156 / (2π) = 9068.2958 inches.
Curiously, another link can be made between these two types of lunar month, and a solar year, and it is to the Metonic period, in days, which is 19 years or 235 lunations, which are 6 939.68865 days. This period is almost equal to 27.32166 x 29.53059 x π x 1000 / 365.242199 = 6 939.8187 days. So the sidereal month can be defined, approximately, as 235 x 29.53059 x 365.242199 / (29.536059 x 1000 x π), simplified to 235 x 365.242199 / (1 000 x π) = 27.31148, or 365.242199² x 19 / (29.53059 x 1 000 x π).
Perhaps a system of keeping track of the movements of the heavenly bodies was designed at some point in the distant past, which brought together the numbers corresponding to various astronomical cycles. This system could then have been used to base the design plans for Giza on.
In these figures we find the repeated use of the square root of three. Perhaps it is because it is close to, and can be approximately equated to, 223 x 365.242199 / (1000 x 47), or to 223 x 29.53059 / (100 x 38).
It's incredible to think that in the context of these lunar connections, the base side of the second pyramid is also compatible with 2000 x 1.6180339887³ = 8472.13595 inches, with 1.6180339887 being Phi. If we take Phi and cube it, and then multiply it by 2000, we get the side of the second pyramid in inches. But then if we multiply this result by 235 / 223 x 4 we get the Great Giza Rectangle length, given by Flinders Petrie as 35 713.2 inches, which then can be multiplied by 9 / 11 to obtain the width of this rectangle, as well as the number of days, approximately, in an 80 year period, which is 365.25 x 80 = 29 220 days. The width given by Flinders Petrie is 29 227.2 inches. And 2000 x 1.6180339887³ x 235 / 223 x 4 x 9/11 = 29 219.02575. And in a similar way, starting from Phi cubed, in inches, we can obtain the value of the side of the Great Pyramid in inches: 2000 x 1.6180339887³ x 30 / 29.53059 x 235 / 223 = 9069.9532. Flinders Petrie gives the side of the Great Pyramid as 9068.8 inches. And then since the side relates to the height via pi and 2, and the height itself relates to 10 000 via the square root of three, we can say that the Great Pyramid height can be approximated by: 2000 x 1.6180339887³ x 30 / 29.53059 x 235 / 223 x 2 / π = 5774.1115, and that the 10 000 that this height relates to via the square root of three can be approximated by: 2000 x 1.6180339887³ x 30 / 29.53059 x 235 / 223 x 2 / π x √3 = 10 001.5456. Richard and Robin Heath found that 10 000 is close to 366 sidereal months in days. 27.32167 x 366 is 9 999.73. Dennis Payne found that a draconic year of 346.6201 can be connected to 10 000: 346.6201 x 100 / 6 x √3 = 10 006.0604. Also, 5 draconic years in days are 1 733.1005, which, divided by 1000, is close to the first few digits of √3, which are 1.73205 As Howard Crowhurst points out (15), the number of hours in a lunation multiplied by 127 and divided by 9 is very close to 10 000. 29.53059 x 24 x 127 / 9 = 10 001.02648. This can also be interpreted as 12 lunations in days x 254 / 9. And if we understand the metre as 10 000 / 254 inches, it relates to a length of 29.53059 x 4/3 inches via a ratio of 1.000102648. There's another amazing connection. If we take the side of the Great Giza Rectangle as 2000 x 1.6180339887³ x 235 / 223 x 4 = 35 712.142587 inches, and then multiply this by 28 / 10 the result is 99 993.999244, almost exactly 10 000. And 28 is a number that is significant in and of itself as a lunar number, 28 days in a lunar cycle, and the inverse of 28 is connected to the mathematical and astronomical patterns we've seen already. It's very close to √3 x 3 000 / (2π x 29.53059) = 28.004633. Which means that to multiply by 28 is almost equivalent to multiplying by √3 x 3 000 / (2π x 29.53059). The 10 000 inches that give us the Great Pyramid height when divided by √3 also approximately give us the Great Giza Rectangle length when multiplied by 2π x 29.53059 / √3 x 30. In fact both the Great Pyramid height and the Great Giza Rectangle length equations benefit from replacing the 10 000 with a slightly greater value, 10 002 or 10 003 in that this produces values closer to Flinders Petrie's measurements. Bailly tells us there was a 10 000 year period used by the Tartars. And we've seen that 10 000 is also approximately connected to these numbers below.

We can also relate the side of the third pyramid, and the height too, to this Phi cubed that defines the side of the second pyramid, and to the 10 000 / √3 inches and 5000π /√3 inches which define the height and side of the Great Pyramid with simple fractions. 2000 x 1.6180339887³ x 30 000 / 254² x 235 / 223 = 4151.5449. And with Phi squared instead of cubed, 2000 x 1.6180339887² x 30 000 / 254² x 235 / 223 = 2 565.7958. Flinders Petrie's dimensions for the side and height in inches are 4 153.6 and 2564 ± 15 or 2580.8 ± 2,0 respectively.
There is also another number which the height of the third pyramid relates to and it is 12³. The height of the third pyramid in inches is 12³ x 10¹⁰ / (254⁴ x Phi) = 2 565.7971. This is because Phi³ x 6 / 1000 x 235 / 223 x 254² = 1728.0034435
This is a nice connection because of the duodecimal system in measure and the importance of the number 6 in both measure and astronomy (the 60 and 600 year cycles). It is less surprising when we see this connection to find the metre being used in connection with a duodecimal system (for example the megalithic yard as 4 x 12 ⁴/ 100 000 metres).


.
Conclusion
The moon provides a lens through which we can look at Giza, and other ancient sites. In turn, Giza interpreted in this way provides a lens through which we can observe the moon, and begin to guess the principles of ancient astronomy. It is mostly though measures expressed in inches that the dimensions can be understood as cycles of time, and also through the metre, when in conjunction with Mars or Venus cycles. The cubit also can express lunar numbers, and when it is near the 20.614 inch mark, it is close to the ratio between solar and lunar years, multiplied by 20. The bases and heights of the three main pyramids, as well as the length and width of the Great Giza Rectangle, are all linked to each other by ratios involving lunar numbers, such as 29.53059, or pi, Phi and the square root of three.
Flinders Petrie wrote:
There does not appear to be any exact relation between their centres, or between the corners; and from the nature and appearance of the ground, and the irregularity of the peribolus walls, it would not seem likely that any connection had been planned. (12)
It's up to the reader to decide whether there is any overall plan to the buildings of the Giza plateau. The many measures and proportions which reveal lunar and other astornomical connections, however, do seem to point to a scheme which was well thought out, intricate, and precisely carried out.
We know that the inch expresses time in days, both at Giza and in European megalithic sites. The width of the Great Giza Rectangle, 29227.2 English inches according to Petrie, encompasses 990 lunations and 80 solar years, which is equivalent to 10 cycles of Venus, and the Chaldean period of 60 years in metres, all in inches. The various units, inches, feet of any kind, metres, are perhaps a way of emphasizing the existence of several cycles in one same length. If the base of the Great Pyramid can be interpreted as the synodic orbital period of Mars in days combined with a lunation, in days, but also the other orbital period of MArs expressed in Saxon feet, this tells us something about a system that couldhave been in place long ago. For example, the ratio between the metre and the Saxon foot can be understood in terms of Mars and the Moon, and the metre can be understood as a way of expressing time, a cycle, involving the Moon in combination with a planet, whether Mars or Venus.
According to Robin Heath and Richard Heath, after working on megalithic sites in England and France,
the practice of day-inch counting leading to a definition of the megalithicyard (32 and 5/8 inches) from the relative lengths of lunar and solar years,that is as a natural metrological consequence of counting days in inches.(8)
This is exactly what we find at Giza. An inch signifies a day, and other lengths seem to be simply particular numbers of inches, accoridng to various astornomical cycles and harmonies.
1 metre is approximately equal to the width of the Great Giza Rectangle divided by 742.1, the number of lunations over a period of 60 years, which is a cycle within which the moon and sun reconcile, known to the ancient world, in particular the Chaldeans and Indians. Also approximately, 1 Egyptian royal cubit is also equal to the width of this rectangle divided by 48 lunations, expressed in inches and days. 1 Saxon foot is equal to the base of the Great Pyramid divided by the sidereal orbital period of Mars 687, in days and inches. 1 metre is equal to the base of the Great Pyramid divided by 780, the Mars orbital period, and a lunation, 29.53059, multiplied by 100, also using days and inches. Perhaps even 1 Roman foot is equal to the base of the Great Pyramid divided by 779, 94, the synodic period of Mars, also in inches and days. Perhaps even the French foot could have been something like the width of the Giza rectangle divided by 7.8 and 29.53059. One type of Egyptian cubit would be the ratio of the solar year to the lunar year, multiplied by 20, again in inches. Likewise with a cubit of 0.525 m, one could think of this same ratio but with a year of 366 days - it's not exact, but close enough.
What this analysis also shows is that irrational numbers, and geometric figures associated with these, like the circle, the square, the triangle, are somehow closely associated with natural time cycles. The irrational numbers such as the square root of 3, pi and Phi in particular, stand out in the analysis of the Giza proportions and dimensions. These numbers, or at least approximations of them, can even be defined in terms of lunar, solar and planetary time cycles. However, their irrational character is also very important, and links our world to the divide world, both from these associations with the workings of the natural world, and from being beyond the caopabilities of human expression. We can never really know the value of the square root of two or three, of pi or Phi. There is no number, which, squared, gives two, or three, or five. The presence of these irrationals links the workings of the natural world to the divine.
Another thing of interest is that it's not necessarily only the moon's cycles with respect to the sun, or Venus or Mars, that seems to come up, but the moon's cycle in relation to the way we see it from earth, between apogees. Le Gentil makes the point in his book "Voyage dans les Mers del'Inde" that the 60 or 600 year cycle is fairly good at reconciling the sun and moon's cycles, but with some error. He notes that this cycle may have had more to do with the cycle of the moon's apogees. For Le Gentil, based on the astronomical tables of the Brahmins which he studied in India, the Saros is a period of 1296 days, which marks out the apogees of the moon. and according to him, all the lunar periods for the ancient astrnomers were designed around the moon's apogee. (see p 338) This is true for the 600 year period as well as for the 248 day period. The 248 day period is slightly mysterious, in that 9 sidereal months are 245.8953 days, almost but not quite 248 days. In any case, this number has not yet been found at Giza. However, the 600 year period does seem relevant at Giza. The width of the Great Giza Rectangle seems to link the precessional cycle of 24 000 years, in days, to half of this 600 year period. For the ancient Brahmin astronomers, surprisingly, the precessional cycle was not 25920 years, but 24 000 years, and accordingly, the annual rate of precession was calculated at 54 seconds, not 50 as it is today. Le Gentil suggests that the Saros is not a period of 3,600 years as traditionally believed but rather a period of 1,296 days, which closely aligns with the apogee of the Moon in his tables.
Le Gentil's work on these numbers from the ancient Brahmin tables is relevant to the study of the Giza pyramids, because these ancient tables tell us how astronomy was done thousands of years ago. There may of course be differences between ancient Egyptian astronomy and the ancient Indian system, but it is fascinating to see how the various cycles were managed, and predictions were, according to Le Gentil, surprisingly accurate.




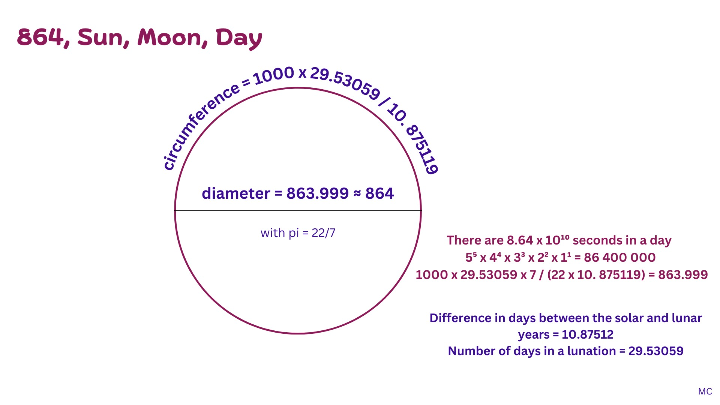
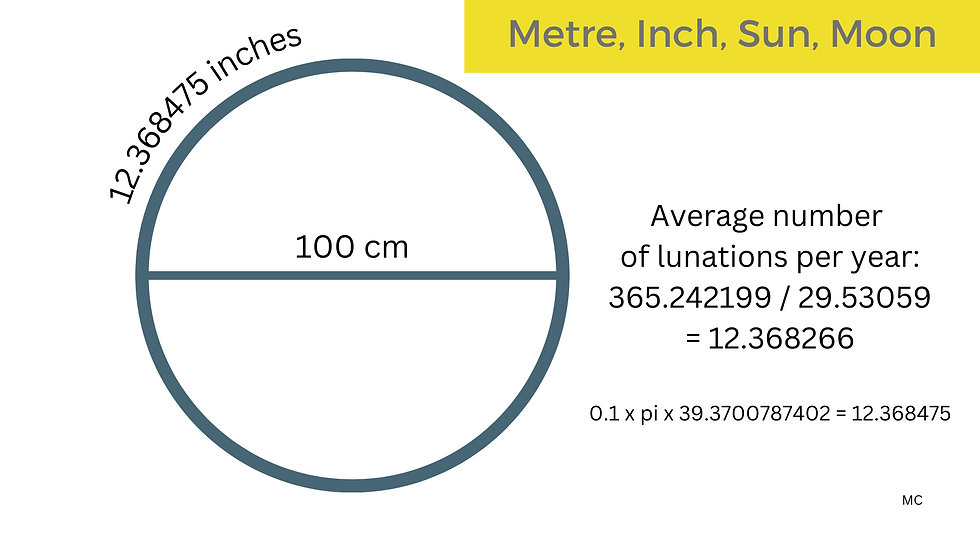

Notes
See Le Gentil's Voyage dans les Mers de l'Inde p 337 and 339, where he writes that the period of 1296 days is for him the Saros period, at the end of which the moon returns to it apogee. (see screenshot in Appendix below)
The period of 248 days is also a period written about by Le Gentil, after which the moon completes a cycle. See in his Voyage p 339
See Irv Bromberg's work on the Hebrew Calendar, Why Divide Hours into 1080 Parts? (utoronto.ca)
Ibid.
Ibid.
See Jim Wakefield's post on the Graham Hancock Message Board here: Venus and the 2nd pyramid - Graham Hancock Official Website
All measures are taken from Sir William Matthew Flinders Petrie, The Pyramids and Temples of Gizeh, 1883, The Pyramids and Temples of Gizeh Online (ronaldbirdsall.com)
Richard Heath & Robin Heath, 2011, THE MEANING OF LE MENEC: A Study of The Moon Using Circumpolar Stars and Sidereal Time, in 4000 BCE
Ibid.
Ibid
See (60) Khafre's pyramid Confirms its Lunar connection, Plus it Memorializes the Metric cubit of Pi/6/25.4 | Dennis Payne - Academia.edu
Sir William Matthew Flinders Petrie, The Pyramids and Temples of Gizeh, 1883 Pyramids and Temples of Gizeh: Ch. 13, Positions and Orientation of the Pyramids (ronaldbirdsall.com)
Bailly writes: "The ancient Persians, who, according to us, are the ancestors of the Chaldeans, had a form of intercalation which spanned a period of 1440 years." Histoire de l'Astronomie Ancienne, Vol. 1, page 13. Histoire de l'astronomie ancienne, depuis son origine jusqu'à l'établissement de l'École d'Alexandrie - Google Play Books
Bailly writes: "The Tartars confirm the antiquity of the time of Fohi, or at least go back to this period. They count in cycles of 60, 180 & 10,000 years." Histoire de l'Astronomie Ancienne, Vol. 1, page 16. Histoire de l'astronomie ancienne, depuis son origine jusqu'à l'établissement de l'École d'Alexandrie - Google Play Books
Crowhurst, Howard, 2011, Carnac the Alignments, p 51
Appendix
Extracts from Guillaume Le Gentil's Voyage dans les Mers de l'Inde (Tome 1):


























https://grahamhancock.com/phorum/read.php?1,1130780
Wow Melissa, you have really hit it out of the park with that Overview of the Moons Role at Giza Blog
Many thanks for including some of my work, the amount of information you have included is stunning , really impressive stuff.