The harmonic series is a mathematical sequence in which all positive unit fractions, starting with 1/2, 1/3, 1/3, 1/4, etc, form a sum.

The first n terms of the series combine to the natural logarithm on n plus a constant, 'γ ', or 'gamma'. While the series itself tends towards infinity, this constant γ remains, and was discovered by Leonard Euler in 1734. Later, in 1790, Lorenzo Mascheroni used this number, so now it is referred to as the Euler-Mascheroni constant. In decimal notation, it looks like this: 0.577272156649.

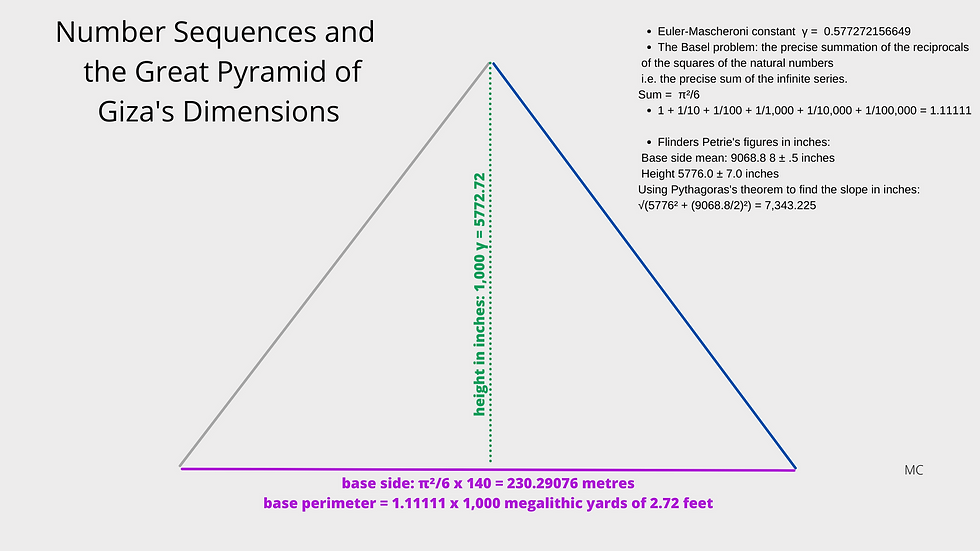
In the context of the ancient world, it is curious how this number is similar to the height of the Great Pyramid of Giza, in inches, as measured by Flinders Petrie: 5,776 ± 7.0 inches.

Ancient Egyptian mathematics, at least what we know of them, are full of fractions with a denominator of 1, written in the form 1/n, or sums of such unit fractions. The Egyptian Mathematical Leather Roll contains a table of unit fractions which are sums of other unit fractions. The Rhind Mathematical Papyrus contains 2/n tables. It's not impossible that long ago in Egypt, there might have been an interest in summing up 1/2, 1/3, 1/4, 1/4, 1/5, and so on, as far as possible, and in finding a pattern in the sequence created. While there is no evidence of this, it is worth considering the possibility, and that if a constant had been found to partly define this sequence, that it might have been somehow encoded in the pyramid.

Dennis Payne has pointed out that there are at least three possible interepretations of the Great Pyramid's height in inches: 5773.5" as x 3 gives 17320.5 , 5773.68" / 792 = 7.29 and 5775" / 280 = 20.625". David Kenworthy has added to this 146.6666 metres. All these interpretations have merit. Here is one more to add: the height of the Great Pyramid as 1,000 times the Euler-Mascheroni constant.

In the context of geometry, it is also curious how close the Euler-Mascheroni constant is to 1/ √3, which in decimal notation can be approximated by 0.5773502692. It might be tempting to draw paralells between the ration of a height and the sides of an equilateral triangle, for example, and the harmonic series itself. Also, the constant e multiplied by 10/3 and the square root of 2 gives 2.721287, the number of feet in a Megalithic Yard.

One subset of the harmonic series is Euler's sum of the reciprocals of squares, or the Basel problem. This would begin like this 1/1² +1/2² +1/3² +1/4² +1/5², and so on. The sum of these fractions is π²/6, as discovered by Euler.

In the context of Ancient Egypt, it is curious how similar π/6 is to the ratio of the cubit to the metre, there being 6 cubits in the circuference of a circle of which the diameter is 1 metre. π/6 = 0.5235987756. There are various values of the cubit, and many of them are in and around this figure in metres, which translates as 20.614125 inches. This connection was made by Schwaller de Lubicz.

To return to the Great Pyramid of Giza, is there a case to be made for the structure to have been designed around number sequences such as these, the sum of reciprocals of squares, and the sum of sums, the harmonic series? Taking the base side of the Great Pyramid as measured by Flinders Petrie, of 9,068.8 inches on average, converted to metres this is 230.3475, (or 230.3479 using Flinders Petrie's inch to metre ratio from the turn of the twentieth century before the inch was readjusted) and dividing it by π²/6, this gives us 140.034. The ratio between the height and base side of the Great Pyramid is 2/π, The height itself would then be approximately 110 x 2/3 π metres. This is in addition to being approximately 10,000 / √3 inches.

A constant derived from another number sequence is to be found, or very nearly, in the ratio between the height and slope of the Great Pyramid. Using Pythagoras's theorem, based on the height and base of the Great Pyramid, the slope should be 7343.225 inches.

2 x 7343.225 / 9068.8 = 1.6194, or close to 34 / 21, two Fibonacci numbers.

David Kenworthy has pointed out that there are 1,111.11111 Megalithic Yards in the Giza base, to include all four sides. 9068.8 x 4 / 1,111.1111 = 32.64769. As a value in inches this is very close to Alexander Thom's Megalithic Yard, which is mostly cited as a value in feet, in or around 2.72 feet. 32.64769 inches are 2.72064 feet. Divided by 1,000, the number 1111.1111 is of course 1.1111 and this can be equated simply to 10/9. It could also be seen as the sum of another arithmetic progression, namely 1 + 1/10 + 1/100 + 1/1,000 + 1/10,000 + 1/100,000, etc.

The Megalithic Yard in feet is of course close to aother famous constant, e, around 2.71828.

Two criticims of these observations can be anticipated: the first is that the ancient Egyptians used neither inch, metre nor Megalithic Yard. The second is that they were rubbish at maths, a view put forward by Otto Neugebauer. Both these criticisms reflect widespread views.

However, here is another way to look at the Great Pyramid of Giza, and the ancient world more generally, in which it's ok to think of the people of those times are pretty smart, and capable of more than the few written remnants of their endeavours that have survived would allow us to believe.

So, perhaps the Great Pyramid contains references to four numerical sequences:

1 + 1/10 + 1/100 + 1/1,000 + 1/10,000 + 1/100,000, etc

1/1² +1/2² +1/3² +1/4² +1/5² etc

1/2, 1/3, 1/3, 1/4, 1/5 etc

and

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 etc

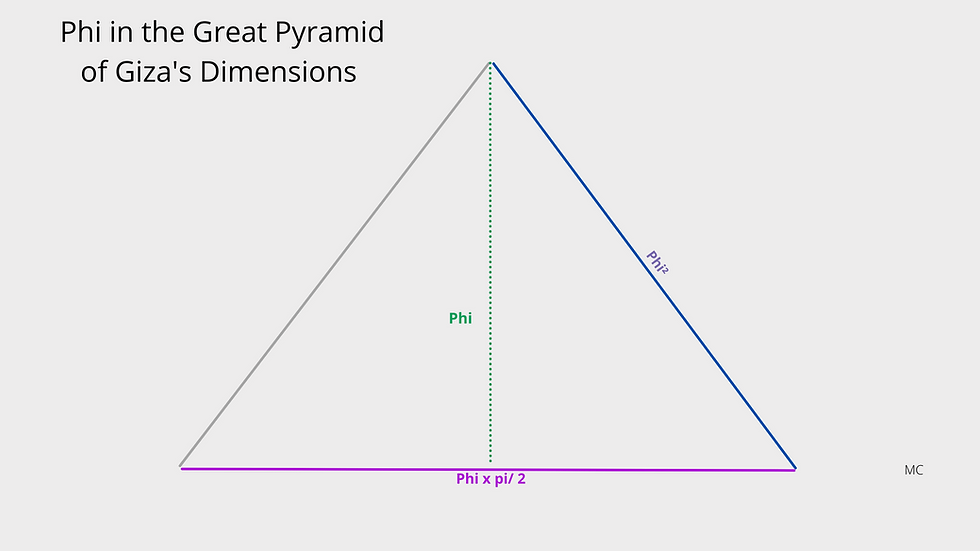
There are two more examples of the Euler constant e at Giza that I'd like to share. One is from the work of Larry Pahl, and concerns the Sphinx, and the other is by Rick Howard, and concerns the angles of the Great Pyramid. Thanks to Larry Pahl for sharing these with me.

In the following video, Larry Pahl demonstrates that not only the golden number but e also are to be found in the dimensions of the Sphinx. This is a fantastic find. Have a look at his video:

(13) Euler and Phi in the Sphinx | TheGreatPyramidAIP - YouTube

With the Sphinx's length as 73 metres and the width as 19 metres, the width multiplied by root 2 and e gives the length. He also finds an e ratio between the two parts of the Sphinx separated by a fissure.

In this article, Rick Howards puts forward his discovery of e within the Great Pyramid: New Page 2 (gizapyramid.com)

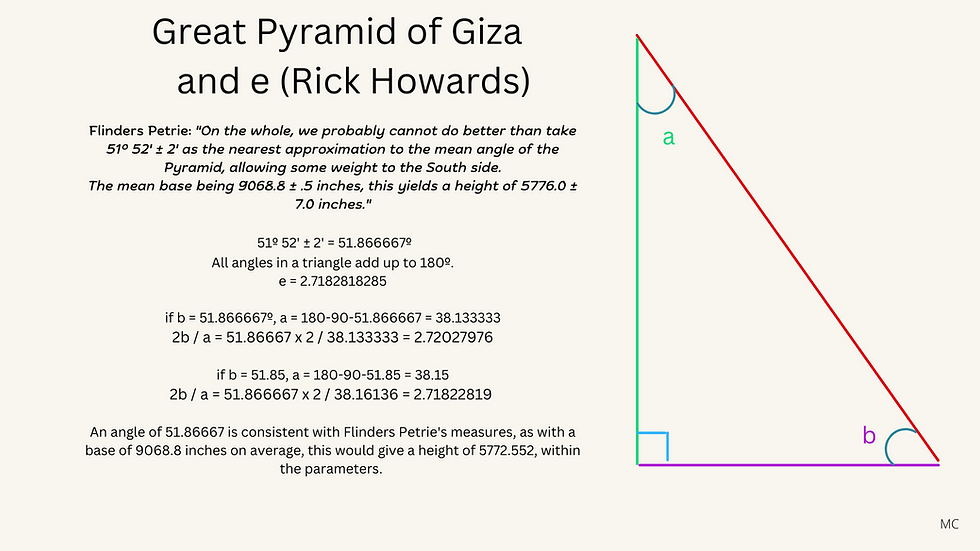
Rick Howards also makes several other very interesting points, including this:

100 x e x Phi = 439.82697

140 x pi = 439.8229715

Which means that e ≈ 14 x pi / (10 x Phi)

Rick Howards's article is well worth a read.

Another thoery involving the Great Pyramid and e is this: Spanish architect Dr. Miquel Perez-Sanchez suggested in 2014 that the pyramid may once have been topped by a sphere, and while he wasn't the first to suggest it, his estimate of the diameter is interesting: 2.7183 Egyptian royal cubits, which he equates to the constant e.