39. An Ancient Liberty: The Imperial Inch and its Relation to the Metre
- M Campbell
- Jun 2, 2022
- 42 min read
Updated: Mar 14, 2024

1. Measuring in inches: “an Ancient liberty”
One consequence of Brexit is that the UK is no longer required to trade in metric units. An article in the Guardian newspaper states:
Since 1995, goods sold in Europe have had to display metric weights and measurements. And since 2000 when the EU’s weights and measures directive came into force, traders have been legally required to use metric units for the sale by weight or measure of fresh produce, which became a recurring issue for Eurosceptics about Brussels’ supposed interference in British life.
While it is still legal to price goods in pounds and ounces, these have to be displayed alongside the price in grams and kilograms.94
The article quotes Boris Johnson, then British Prime Minister, as saying he “claimed that measuring in pounds and ounces was an “ancient liberty””2. But just how independent from the metric system is the imperial system, and how do the two systems relate to each other? While most countries discarded their traditional measuring systems over the last century or two in favour of the metric system, designed by French revolutionaries, only a small handful have chosen to keep theirs. While the language of the long-lost British Empire has remained ubiquitous and influential in the world, the system of measure that underpinned the empire's trade and engineering projects has largely been replaced by the system created by the great rival empire of the time, France. The imperial system is now used only in the UK, the USA, Myanmar and Liberia.
Despite this dwindling popularity across the world, the inch and the foot have had great champions, such as English metrologists John Michell and John Neal. One reason for their enthusiasm is that their research has found the English inch, foot and yard to be part of an extremely old and sophisticated system of measure, designed by people well versed in surveying and astronomy. The foot and the mile are widely acknowledged to be very old units of measure, derived from a reasonably accurate estimate of the circumference of the earth (“geodesic”). The average of the polar and equatorial circumferences is very close to being 125/10 = 24,883.2 miles. Another researcher, Robin Heath, has suggested the equatorial circumference was divided by the number of days in a solar year, and that figure was then divided by 360,000, to produce one small unit of measurement, the English foot. Hence, the equatorial circumference of the earth is 365.242199 x 360,000 =131,487,191.64 feet, or 24,902.877 miles 95. The exact distance around the equator is estimated today to be exactly 24,901.461 miles, and around the poles is 24,859.734 miles (producing an average of 24,880.5975 miles).
Another researcher, has found intriguing connections between the mile and the earth: Hugh Franklin has linked the value of the circumference in miles to pi, the ratio between a circle’s circumference and diameter. In his article “Earth, Pi, Miles and the Barleycorn”, he points out that the number 24,902.31984, which is very close to the contemporary figure for the equatorial circumference of the earth in miles, is in fact √(π3 x 20,000,000). A circle with a circumference of 24,902.31984 miles will have a diameter which can also be the diagonal of a square. The square will have a side of 24,902.31984 /(√2x π) miles, and the area of this square will be 10,000,000 π square miles. This square would be equal in area to a circle with a diameter of 10,000,000 miles. This would suggest that the equatorial circumference of our planet, via the geometries of the circle and the square, gave rise to the mile itself, as a unit of measure. The circumference of the earth as a value in miles is equated to a square with an area of 10,000,000 π square miles. It’s worth noting that in this model, actual (calculator) pi is used, not a rough approximation such as 22/7.
So, approximately,
one mile = earth’s equatorial circumference /( √(π3 x 20,000,000)
= √(10,000,000 π) x √2 x π /earth’s equatorial circumference
and the equatorial circumference of the earth
= 365.242199 x 360,000 =131,487,191.64 feet, or 24,902.877 miles
Historical astronomy is connected to the history of measure. There is a link between the mile and the cycles of the sun and the moon also. One lunation in days, 29.53059, divided by the average difference in days between the lunar year and the solar year, 10.87512 days, multiplied by 7,000/36, is 5,279.996. There are of course 5,280 feet in a mile, and if this is taken to be a value in feet, it’s very close to a mile.
5,280 x 10.87512 x 36 / 70,000 = 29.5306
And so one mile, in feet, can be defined as 70,000 lunations / (36 x the difference in days between solar and lunar years). Consequently, earth’s equatorial circumference in feet
= 70,000 lunations x (√(π3 x 20,000,000) / ( 36 x the difference in days between solar and lunar years)
= √(10,000,000 π) x √2 x π x 5,280
and the equatorial circumference of the earth in miles
= 365.242199 x 1,296 x the difference in days between solar and lunar years / 7 lunations
and the meridian circumference of the earth
= 1752 x 10,000,000 lunations / ( 3 x the difference in days between solar and lunar years x 176) inches
The imperial system of measure offers many intriguing possible connections to geodesy, geometry, and astronomy that are not easily dismissed.

2. Measuring in metres: an (almost) universal measure
Making an accurate, durable and stable standard of measure for a city, yet alone a whole country, is notoriously difficult. It requires a stable, central seat of power for a region. Apart from the political difficulties in creating an internationally adhered to system, standards made of wood or metal shrink and expand, chip and bend, burn down, rust after shipwreck, or are sent across the great ocean on ships that are captured by pirates (all these things have happened to measuring standards!). As a result, scientists started falling back on light waves and other highly regular and predictable microscopic phenomena to define standards of measure against. But exactly what length of a beam of light's journey should be adopted to make a new standard?
In late 18th century France, various ideas were explored but in the end, it was agreed the new unit should be derived from the polar circumference of the earth. The imperial system being popular and reliable, as well as probably derived from the size of the earth, the United Kingdom wasn’t interested in adopting any new measure. It had confidence in its own system of measure, and in its own empire; and then there was also the old rivalry between France and England, which had been kept alive by recent wars between the British and French empires. In any case, in UK, the political will to adhere to a universal system created by the French wasn’t there. Yet there had been an appetite for a universal measure in Britain for some time in the scientific community. John Wilkins, a fellow of the Royal Society, had written in 1668 96:
The several Nations of the World do not more differ in their Languages, than in the various kinds and proportions of these Measures. And it is not without great difficulty, that the Measures observed by all those different Nations who traffick together, are reduced to that which is commonly known and received by anyone of them; which labour would be much abbreviated, if they were all of them fixed to any one certain Standard. To which purpose, it were most desirable to find out some natural Standard, or universal Measure, which hath been esteemed by Learned men as one of the desiderata in Philosophy. If this could be done in Longitude, the other Measures might be easily fixed from thence.
The French revolutionary metric project could almost have been announced by these words. Indeed, Talleyrand wrote to the Assemblée Nationale in 1790:
Here, then, is the draft decree that I am submitting to the Assembly.
DRAFT DECREE.
The National Assembly desiring for the whole of France to enjoy forever the advantage which should result from the uniformity of weights and measures, and desiring that the ratios of the old measures to the new ones be clearly determined and easily grasped, decrees that His, Majesty will be begged to give orders to the commissioners chosen by her for the establishment of the assemblies of departments and districts so that they obtain from all the municipalities comprised in each department and that they bring back to Paris a perfectly exact model of the different basic weights and measures that are in use there. Then decrees that the National Assembly shall write a letter to the Parliament of England to engage it to co-operate with France in fixing the natural unity of measures and weights; that consequently, under the auspices of the two nations, commissioners of the Academy of Sciences of Paris will meet in equal numbers with the chosen members of the Royal Society of London, in the place which will be judged most suitable, to determine at the latitude of 45 degrees the length of the pendulum, and to deduce from it an invariable model for all the measures and for the weights; that after this operation carried out with all the necessary solemnity, His Majesty will be requested to instruct the academy of sciences to fix with precision, for each municipality of the kingdom, the ratios of their old weights and measures with the new model , and then to compose, for the use of each of its municipalities, usual and elementary books, where all these proportions will be clearly indicated. Decrees, moreover, that these elementary books shall be addressed at the same time to all the municipalities to be distributed there profusely; that at the same time a certain number of new weights and measures will be sent to each municipality, which will be distributed free of charge by them to those whom this change would constitute too heavy an expense; finally that, six months only after they are sent, the old measures will be abolished and replaced by the new ones.97

While Talleyrand’s exact proposal, with the pendulum, was not adopted, it’s spirit struck a chord. Soon after, the creation and implementation of the metre as a division of the meridional circumference of the earth was agreed upon. Ironically it was after consultation with other countries including the US and the UK that the French decided against the pendulum measure and in favour of the land measure. With the introduction of this new unit, finally all the old ways, with their corruption and confusion, could be left behind, in this brave new world that was being created. Also, this new metre wasn't so scary really, just a slightly longer version of the old familiar toise of three French feet, re-jigged into a brand new decimal system. Decimal systems were far more in keeping with the revolutionary spirit than the old sexagesimal one, and had been proposed by the Abbé Mouton long before. In fact, it was even hoped that a new decimal system of measuring time would be adopted.
Ironically, a decimal system had excited long before in England, as opposed to the duodecimal imperial system, based on the number twelve, with a unit close in size to the modern metre.98 In his entry on "Weights and Measures" in the Encyclopaedia Britannica (1911), Flinders Petrie claimed that "the Belgic foot of the Tungri is the basis of the present English land measures, which we thus see are neither Roman nor British in origin, but Belgic." 99 Land measures still in use today, from the rod to the mile, were once expressed in terms of multiples of a different foot to the one we have today. He then goes on to say of the Belgic foot:
It is remarkable how near this early decimal system of Germany and Britain is the double of the modern decimal metric system. Had it not been unhappily driven out by the 12-in. foot, and repressed by statutes both against its yard and mile, we should need but a small change to place our measures in accord with the metre.100
What remains of the predecessor of the imperial system in Britain is indeed decimal: a mile is 8 furlongs, but was once 10 furlongs. A furlong is 10 chains, a chain is 10 fathoms. 400 feet of 13.2 inches fit into a mile, and this foot of 13.2 inches gives a yard of 39.6 inches, which is 54 x 0.733333 inches. A unit of about 40 inches was in use, called the yard and full hand, and a third of that would have been 13¹/³ inches. Flinders Petrie explains:
Turning now to England, we find the commonest building foot up to the 15th century averaged 13·22. Here we see the Belgic foot passed over to England, and we can fill the gap to a considerable extent from the itinerary measures. It has been shown that the old English mile, at least as far back as the 13th century, was of 10 and not 8 furlongs. It was therefore equal to 79,200 in., and divided decimally into 10 furlongs, 100 chains, or 1000 fathoms. For the existence of this fathom (half the Belgic pertica) we have the proof of its half, or yard, needing to be suppressed by statute (9) in 1439, as “the yard and full hand,” or about 40 in.,—evidently the yard of the most usual old English foot of 13·22, which would be 39·66. We can restore then the old English system of long measure from the buildings, the statute-prohibition, the surviving chain and furlong, and the old English mile shown by maps and itineraries, thus:—
foot, 3=yard, 2=fathom, 10=chain, 10=furlong, 10=mile
13·22 39·66 79·32 793.2 7932 79,320
Such a regular and extensive system could not have been put into use throughout the whole country suddenly in 1250, especially as it must have had to resist the legal foot now in use, which was enforced (9) as early as 950. We cannot suppose that such a system would be invented and become general in face of the laws enforcing the 12-in. foot. Therefore it must be dated some time before the 10th century, and this brings it as near as we can now hope to the Belgic foot, which lasted certainly to the 3rd or 4th century, and is exactly in the line of migration of the Belgic tribes into Britain.101
Flinders Petrie’s analysis raises the question of whether the ancient liberty that Boris Johnson referred to might not also apply to the use of the metre.
In any case, while in France it was ‘out with the old and in with the new’, strong conservative principles reigned on the other side of the Channel. The suggestion of adopting the metre was made in the British parliament, but the response was lukewarm, and the proposal soon forgotten. Replacing the imperial system must have seemed about as horrific as chopping off your king and queen’s heads. Napoleon’s expansionist policies did nothing to warm the British to the new metric project in the aftermath of the revolution. So how was it that, in a strange twist of fate, a couple of centuries later, the measures indigenous to the UK were actually redefined in relation to this same metre?
3. The relationship between English and French measures from the 17th century
By the twentieth century, the history of the inch, foot and yard had become forever intertwined with the history of the metre. The reason seems simply to have been that the surviving standards for the yard and foot were not stable or trustworthy, though it seems hard to believe the UK was incapable of producing a good new standard. It is true, however, that designing, and keeping safe, a durable and precise standard of measure, compatible with the demands of science, had been problematic. The 17th century was a time of great energy in science, and already in the second half of the century the problem of reliable standards had become evident, and an obstacle to scientific progress.
In 1666, the Great Fire of London destroyed standards in the Guildhall. and just the following year, in 1667, the main standard for the toise in Paris, a metal bar in a courtyard of the Châtelet, was accidentally bent out of shape. The Parisian authorities replaced it with a slightly different length, and stuck to their guns despite the protests. It seems that a a slightly different standard for the London foot was also used to replace the one in the Guildhall, according to Matthew Raper, though probably not intentionally so. While there were other standards in London (for example Elizabeth's Exchequer Standard Yard of 1588) and Paris (for example the Toise de l’Ecritoire, or the Aune des Marchands, Merciers et Grossiers, of 1554, an aune being an ulna or yard), the accidental damage caused to the standards in both cities underlined the difficulty in keeping and enforcing a single precise value for the foot, be it French or English. To find out how long the London foot would have been before the fire, Raper wrote “we have nothing left whereby to discover its true magnitude, but the measures others have taken of it, and those which have since been taken of such magnitudes as Greaves had compared with his copy of it”. 102
The measure of the Paris foot, which Greaves received from Mons. Hardy, was taken from the old standard in the Châtelet and contained 1068 such parts as his London foot contained 1000. These numbers are in the proportion of 1065.4 to 997.57; therefore, if the new standard did not differ from the old one (and no such difference appears to have been intended), Greaves’s London foot must have been 2.43 parts in 1000 shorter than Graham’s. All these comparisons shew Greaves’s measure of the London foot to have been shorter than Graham’s. (...) The three more immediate comparisons of Greaves’s measure with the Paris foot, are by the measures of Auzout, Desgodetz and Hardy, which afford as clear a proof as can well be expected in this matter, that his measure of the iron standard was about 2 parts in 1000 deficient of Graham’s London foot.103
This means that in modern inches, the pre-Great Fire of London foot measured 12 - (12 x 2.43 / 1000) = 11.97084 inches, or more conservatively, using the 2 parts in 1000 instead of 2.43, 11.976 inches. So to convert to pre-1666 values, the English foot can be multiplied by 0.998.
Scientists were left to their own devices to come up with good physical copies of the national standard, and their work depended on their particular version of the unit, made by a particular craftsman. When Newton wrote his System of the World104, he was using French pied de roi, based on Picard’s work, but it is not clear if he had access to precisely the length of the pied Picard was working with. Picard’s standard, upon which all his work was based, was lost a few decades after, and there is, to this day, no trace of it, and it’s difficult to assess his measuring work. A small difference on a ruler can make a big difference on a large scale.
As a result, the French scientist and explorer La Condamine had to have his own standard for the Paris foot made, based on as accurate a reading of the crude metal bar at the Châtelet as was possible, in preparation for an expedition to measure the world (and verify Newton’s theory of the shape of the earth in the process). The ruler La Condamine took to Peru became, on its return to Paris, the main standard for the Académie des Sciences, and for Paris, until the French foot was replaced by the metre.
Even in the 18th century, it was not a given that even top scientists would agree on the precise length of a standard. In 1760, Matthew Raper wrote about the pied de roi in relation to the English foot:
The Paris foot is one sixth part of the toise in the Châtelet; which was renewed in the year 1668, and the new standard has continued in use ever since. In the year 1742, the Royal Academy of Sciences of Paris, at the request of the Royal Society of London, sent over a measure of half a toise of the Châtelet, from which Mr. Graham determined the proportion of the Paris foot to that of London to be as 1065.41²/³ to 1000. Mons. le Monnier, of the Royal Academy of Sciences, from the same originals, found their proportion as 864 to 811, or as 1065.351 to 1000. 105
The way the standard for the metre was designed, and the way the use of the new metre was implemented right across France, brought about the beginning of the end of the long uncertainty that had surrounded the value of the national standard for so long. The new metric standards were made of an alloy of 90% platinum and 10% iridium, which had the benefit of being durable and hard. Just in case of the slightest alteration, the metre was defined by the distance between two engraved lines, not the extremities of the bar.
By contrast, national standards of measure were still problematic in the UK and USA, right through the nineteenth century. In 1893, in the USA, the Mendenhall Order changed the fundamental standards of length and mass from the customary standards based on those of England to the metric standards. Soon after, the UK followed, and the imperial units were made to align the system to the metric system, legalised in 1897 in the Weights and Measures Act. While the UK might perhaps have simply designed a new stable standard of its own, it was decided that the French standards should provide the basis for the inch, foot and yard.
The length chosen for the new stable metric standard was simply the old mètre des archives. This corresponded to the length of the bar which had been provisionally placed in the French National Archives on 22 June 1799, soon after the king had been beheaded, at which point the use of a royal foot seemed desperately outdated. Méchain and Delambre had not yet finished their painstaking work measuring the meridian between Dunkirk and Barcelona, so the idea was to use this provisional metre till such a time as a new, properly geodesic metre could be designed. As is often the way with provisional arrangements, the mètre des archives became permanent, and remained the legal and practical standard for the metre in France, and subsequently for most of the world, after 1867.106
However there is quite a difference between the lengths, as measured in inches, of the first metre agreed upon, 39.3827 inches, and the variations on this measure interpreted in inches of the late nineteenth and early twentieth centuries, much closer to 39.37 inches.
With this whole new level of precision and durability, getting the correct ratio between inch and metre, whatever the criteria for that may be, should have been more straightforward that in the 16th and 17th centuries. Yet, the historical ratios between metre and yard abound, all through the 19th century, and the beginning of the 20th century. Was there an intended ideal ratio between the metre and the yard?

The ratio between the English or imperial yard and the metre
In the early twentieth century, British scientists adjusted the length of the yard to a certain ratio of the French metre derived from a very thorough examination of several metric standards. In an article published by the Royal Society in 1928, entitled "A New Determination of the Ratio of the Imperial Standard Yard to the International Prototype Metre", by J.E. Sears, W.H. Johnson and H.L.P. Jolly, 107the metre is defined as 39.370147 inches. The method used involved not an ideal notion of what the ratio ought to be, but a thorough examination of the actual French standards, using a neutral standard with graduations that approximated the yard and metre, "32 main intervals being closely equivalent to one yard and 35 to one metre."108While 36 inches divided by 32 and multiplied by 35 make 39.375 inches, this is quite a bit longer than the authors' proposed 39.370147 inches. The third smallest graduations on the standard are 0.125 inches, and so there are 288 of these 0.125 inch units in a yard and 315 of these in a 39.375 inch metre. Smaller subdivisions of 1/40 and 1/200 inches also divide perfectly into 36 and 37.375. The fractions used, 288/315, or 64/7, are the same ratio C. Mauss used.

1927 New Determination of Ratio of Yard to Metre
To put that in context, from the 1897 Weights and Measures Act the definition of the metre in inches was 39.370113 inches. Before that, in 1836, a book by Olinthus Gregory gives 39.37079 inches to the metre, and in 1816 Patrick Kelly defined the metre as 39.371 English inches.
Originally, the metre was defined as 3 French feet and 11.296 lines of the Toise of the Academy, in 1799, and in relation to the English inch, it was a little longer than the current metre, at 39.3827 inches. As part of Méchain and Delambre’s 1810 report, the relationship was examined between the English measure and the platinum metre, the iron metre and the toise commissioned by Bouguer, at a temperature of 12.15 degrees centigrade, the platinum metre contained 39.3781 English inches; and the iron meter, 39.3795. “These lengths, reduced to the temperature of ice, according to the law of the expansion of metals determined by experiment, give results which only differ from each other by about an inch, and whose mean value is 39.3827 English inches. equivalent to 1 French metre.” 109
In Robert Hussey's 1836 article, "Essay on the Ancient Weights and Money110, he writes the English foot is to the [metric] French foot [one third of a metre] as 10,000 to 10,659. He deduces this from the Mémoires de l'Institut, Base du Système Métrique 10. In this account by the creators of the metric system, the metre is clearly stated as 39.3827 inches, being also 3.07861 French Feet, or 443.32 lines, or 0.513074 toises. One line is a 1/144th part of the French foot. In a footnote in his Appendix on the Roman foot 11 , Hussey writes:
As calculations in French measures often occur here, it will be well to state at once the proportion between the French and English. The English foot is to the French as 10000 to 10659. This is deduced from Mem. de l'Institut, Base du Système Métrique, vol. iii. p. 470, where the English foot is compared with the metre, and the latter is proved to be equal to 39.3827 English inches, or 3.2818916, &c. English feet. In the same vol. p. 557, the metre is reckoned equal to 443.32 lines, the line being the 1/144th part of a French foot. Hence the metre is equal to 3.07861 &c. French feet; from which the proportion above given follows. Eisenschmidt (p. 94.) gives the proportion 1000 to 1066 : De Romé de l'lsle 10000 to 10646. In 1742 a comparison between the two feet was made, and the proportion settled as 10000 to 10654. See Philosoph. Trans. 1742. p. 105. But in 1768. Maskelyne (then Astronomer Royal) entertaining some doubts about the correctness of this proportion, caused a new comparison to be made : and the result was that the toise was found to be equal to 76.734 inches of the brass standard of the Royal Society, at the temperature 620 Fahrenheit. This gives the proportion between the feet 10000 to 10657, differing but .0002 from that of the French calculators, which is taken here. See Philosoph. Trans. 1768. p. 326.
This note gives a good idea of the amount of change, and confusion, that occurs between two recent and well-documented units such as the English and French feet. In 1768, 1 toise was worth 76.734 inches, so a French foot was 12.789 inches, and converted to metres with the 144 lines to the French foot and 443.32 lines to the metre, this gives a metre of 39.3723575 inches. But a metre of 39.3827 inches, divided by 443.32 and multiplied by 144, gives 12.792359 inches for the French foot.
Hussey also quotes the ratios of several researchers, such as De Romé de l'Isle, who has 10,000 to 10,646; Maskelyne has 1 toise = 76.734 inches (1768), so the ratio is 10,00 to 10,657. Henry James gives 3 English feet as 0.914391792 metres, which means a metre of 39.370432144 inches. This is the same ratio which the French metrologist Guilhiermoz was using in 1919.111
An article by C. Mauss 112 gives an English yard worth 914.2857 mm and a foot of 304.7616 mm. It follows that he is using a conversion of 1 metre = 39.3750393752 inches for the foot, and 39.375 inches for the yard. He was probably using 39.375 inches for both, and rounded the value for the foot slightly, or even made a typo, as a third of the yard value Mauss uses should read 304.76190476 mm.
Curiously, the authors of the 1927 Royal Society article, mentioned above, also pre-suppose a 39.375 inch ideal measure for the French metre as a starting point, despite their settling on a different figure after careful analysis of various physical standards. This is apparent from their method, in that they used a ruler with 32 intervals of 1 1/8th inch on the yard and 35 of these intervals in a metre of 39.375 inches, which is taken to be "a length closely equal to one metre, the difference of approximately 0.004 inch being conveniently measurable by the direct use of an ordinary comparator microscope with a micrometer eyepiece".
These references to a 39.375 inches value for the metre are very intriguing. It is found in the work of C. Mauss, in the Royal Society article of 1927, in a reference to Cagnazzi by Hussey, and in Algernon Berriman’s book on ancient metrology 113. It is also central to independent research by Jim Alison, Stephen Dail, David Kenworthy, Richard Heath, and others. The main reason for this is that it relates easily to a lunar month, usually rounded to a value of 29.53125 days, and to other numbers in the canonical system, such as 5040, Plato’s number, and 181 440, the Ninevah constant.114 If a Roman foot is considered to be 11.66667 inches, a digit, or 16th part of this foot, can be valued as 0.729166667 inches, and there are 54 such digits in a metre of 39.375 inches, and 45 in a Megalithic Yard of 32.8125 inches.
There is however no mention of this ratio in the work on the determination of the metre by Delambre and Méchain, which contains two chapters on the comparison between the metre and the English measures in Volume 3. It is a very appealing ratio, in that it offers a simple, user-friendly conversion ratio between the metre and the English inch.






Extract from C. Mauss’s essay on ancient measures: L’Eglise de Saint-Jérémie a Abou-Gosch, Observations sur Plusieurs Mesures de l’Antiquité.
We since have had various historical ratios between the metre and the yard, foot and inch (not including the US Survey inch and yard, which in any case are on their way out). Specifically, the metre has been valued at 39.3827 inches, 39.370432144 inches, 39.370147 inches, 39.370113 inches, 39.37 inches and 1/254 = 39.3700787402 inches, as well as, unofficially, 39.375 inches.
By 1927, a year before the article for the Royal Society was published, the International Bureau of Weights and Measures had adopted the 1908 light-wave definition of the metre. This is still used today to define the old mètre des archives in terms of light,. The most recent definition of the metre in terms of light was made in 1983, by international agreement, as the length of the path travelled by light in a vacuum in 1/299,792,458 of a second.
By 1930, the British Standards Institution had adopted a different length for the inch altogether: an inch of 25.4 mm based on the metre, so a metre was worth 10,000/254 = 39.3700787402 inches. The Commonwealth Science Congress confirmed this is 1946, acknowledging that the yard was now 1.7 millionths of an inch longer than the old imperial inch, and 2 millionths of an inch shorter than the old US inch. The international inch has been exactly 25.4 mm since July 1959, and since then the international yard has been 0.9144 metre. The American inch was changed by 2 millionths of an inch and the UK inch by 1.7 millionths of an inch, so that the new international inch falls mid way between the old UK and US inch.
Between 1901 until 1959, the American National Bureau of Standards was using the ratio of 1 yard = 3600/3937 m, so 1 metre = 39.37 inches but in 1959 the definitions were changed by international agreement to be 1 yard = 0.9144 m, so 1 metre = 10,000/254 inches. The revolutionary metric system had become the basis for the imperial system, and the imperial inch was allowed to change in length very slightly. It seems that despite centuries of stability, the value of the inch, in and of itself, came second to the ratio of the inch and the metre.
Trying to interpret pre-2oth century measures expressed in English or imperial feet or inches can become a bit of a headache, because of the number of values given to other units, from the Roman foot, to French foot and to the metre.
The figure Gosselin gives for the Roman foot seems to fit well with a 0.729166666 inch digit, if his 0.296296296 metres are converted to inches with a 39.375 inch metre: multiply Gosselin's figure by 39.375, divide by 16 (there are 16 digits in a Roman foot) and there's the digit of 0.7291666666 inches. But Gosselin's Roman foot is given as 0.9724 decimal parts of the English foot, so that the Roman foot is here, in inches, 12 x 0.9724 = 1.6688, and the digit 0.7293 inches. However, the value given in metres for Cagnazzi is 0.29624, which converts, using Hussey's 39.3827 inches rate to the metre, to 11.666731048 inches.
Taking the 16 digits of a Roman foot against the 12 inches of an English foot, 0.72916666667 x 16 / 12 = 0.972222222. Cagnazzi's Roman foot is 0.9722 parts of an English foot. 0.9722 x 12 = 11.6664 and 0.972222222 x 12 = 11.666666666. The conversion rate of 39.375 inches for a metre is full of possibilities, yet it does not seem to ever have been an official rate. With it, the metric system, the imperial system, as well as various ancient measures such as the Persian and Egyptian, at least according to Mauss, seem to come together into one system. One other nice connection to be drawn from a 39.375 inch value for the metre is simply that 39.375 x 9 / 12 = 29.53125, close to the value in days of a synodic month. Despite all these interesting connections between the English system and the metre, provided by 39.375 inches for the metre, another value was picked, which we have still today. With the new ratio between inch and metre, these theoretical connections created by a 39.375 inch metre vanish.
Metric, Imperial, Egyptian
A metre of 39.375 inches offers some intriguing numerical connections between the metric and imperial systems. For example, for C. Mauss, who uses this value in his work researching Middle Eastern ancient measures, the English yard is one seventh of 6.4 metres. A value of 6.4 metres relates to the yard (of 36 inches) as 16/90. While Mauss connects the English yard and foot to Persian measures, he might also have connected them directly to the French, and said that this same yard was 1 metre (of the 39.375 inch kind, which he was using), x 9/10 x 64/63. In fact 36, the number of inches in a yard, is 40 x 9/10, and if there are 40 x 9/10 inches in a yard which itself is 9/10 x 64/63 metres, it follows there are 40 inches in 64/63 metres (of the 39.375 inch kind). While the modern metre is valued at 10,000/254 inches, this conversion used by Mauss, of 39.375 inch per metre, is 63/64 x 40 inches. Curiously, 64/63 is a ratio associated with Ancient Egypt: the Eye of Horus. This is according to a theory by Egyptologist Georg Möller, who took the various components of the symbol to be fractions of a hekat, with just 63/64 left as a remainder.
A seventh of 6.4 metres is a yard, or 36 inches. 7 yards are also an Egyptian Royal Cubit of 20.625 inches, multiplied by 144/55 x 14/3. The fraction 144/55 is an approximation of Phi squared using Fibonacci numbers. Alternatively, using a value of 20.6181818 inches for the Egyptian Royal Cubit, and a different approximation of Phi squared with other Fibonacci numbers, 55/21, then 7 yards are 20.618181818 x 55/21 x 14/3. Or to simplify, 36 inches x 3/2 x 55/144 are 20.625 inches, and 36 inches x 3/2 x 21/55 are 20.618181818 inches. And the 20.625 inch Egyptian Royal Cubit multiplied by 10/2 and divided by 55/21 for Phi2, or the 20.6181818 inch cubit x 10/2 and divided by 144/55 for Phi2, gives a 39.375 metre. So 3/2 x 10/2 of a yard (or 270 inches), multiplied by 21/55 x 55/144 is a metre of 39.375 inches. A length of 270 inches divided by both types of Fibonacci Phi squared approximations, 144/55 and 55/21, gives the metre of 39.375 inches. The 20.618181818 inch Royal Egyptian Cubit is a yard and a half, or 54 inches, multiplied by 21/55, and the 20.625 inch
Egyptian Royal Cubit is 54 inches x 55/144.
Seven yards can be written as the Egyptian Royal cubit x Phi squared (using 144/55 for a 20.625 inch value and 55/21 for a 20.618181818 inch value for the cubit), x 66/10, divided by 99/70 (an approximation for the square root of two) . Or simply, 7 yards are 132 digits of 0.729166667 inches, multiplied by Phi squared (using 144/55).
Since a 39.375 inch metre multiplied by 55/21 and 2/10 is the 20.625 inch Egyptian Royal Cubit, 7 yards are a 39.375 inch metre multiplied by Phi squared, 28/30, and Phi squared again, with one value for Phi squared at 144/55 and the other 55/21. And 270 inches divided by these two kinds of Phi squared approximations make a metre.
A 39.375 inch ideal metre contains 54 Roman digits of 0.729166667 inches. This digit is, like the imperial measures and the metre, also geodesic, and goes 2,160,000,000 times into a particular value of the circumference of the earth (a polar circumference of 24,857.95454545 miles), 45 times into a Megalithic Yard of 32.8125 inches, 20 times into the remen of 14.583333 inches, 18 times into the Northern foot of 13.125 inches, and 16 times into the Roman foot of 11.666667 inches. All these units can also be valued slightly differently, however, for example a Roman foot of 11.664 or 11.58 inches, etc, and perhaps the digit’s value can be adjusted to fit a contemporary metre of 39.3700787402 inches. A 54th part would be 0.7290755322259 inches, fitting 2,160,000 000 times into an ideal 40,000 km polar radius (ideal, because the polar circumference is usually valued as just a little longer than 40 ooo km, at around 40,007.863 km.115
The 20.625 inch Egyptian Royal cubit works with a 0.7291666667 inch digit, if you apply 99/70 as an approximation of the square root of 2. The Royal Egyptian cubit and the digit, as 20.625 inches and 0.729166667 inches respectively, can be linked like this: cubit x 49,500 / 1,400,000 x 9,800/9,801 = digit. The Neal / Michell value for the Egyptian Royal Cubit of 20.618181818 inches, can be thought of as 25,920 x 54 x 0.7291666667 / 49,500 = 20.6181818181. (This is because the link between these two Egyptian Royal cubits, the 20.6181818 inch one and the 20.625 inch one, is 9,801/9800 x 4,375/4,374.) So we could define the digit of 0.7291666667 inches as simply 25,920 ancient metres divided by 49,500, and multiplied by 4,375/4,374 (ragisma) and 9,801/9,800. Or, to adjust it slightly, the same can be done but with modern metres. The modern value for the metre is the 39.375 inches x 8000/8001.
Another, purely theoretical, link between the metre and inch could be this: a square with sides of 21/55 x 21/55 x 55/144 = 0.0556818181 inches has a diagonal of 2 millimetres of the 39.375 inches metre. i.e. 0.7875 inches. Here all the approximations are used instead of Phi squared and the square root of two. In the same way, we could think of the remen as 100 x 21/55 x 21/55 inches, and the Egyptian royal cubit is the remen times 99/70. A circle with a diameter of 20 x 144/55 metres, which is 100 Egyptian royal cubits of 20.6181818 inches, would have a circumference of 6 480 inches, or 540 feet, with pi = 22/7.
A rod of 198 inches can be interpreted as 7 x 10.8 x 55/21 metres of 39.375 inches, which brings in the numbers 7, Phi squared and the number 108, important in historical measure and astronomy, especially in India, and the moon’s radius is 1080 miles. 3/2 x 10/2 of a yard (or 270 inches) x 21/55 x 55/144 = 39.375 inches. A length of 270 inches divided by both types of Fibonacci Phi squared approximations, 144/55 and 55/21, gives the metre of 39.375 inches.
20.625 x 2.6181818 x 5 = 270.
Ancient Egyptian measures show links to the metre of 39.375 inches, as well as to imperial measures, such as the inch and the yard.
Metre, Inch, Sun, Moon: Measure as Expression of Movement
We’ve seen that a metre can be regarded as significant in terms of historical metrology, as one of many units of measure linked to others by simple fractions, that is to say, as part of a system. There are several reasons why the number 39.375 might be significant in itself, and that the metre might be understood as a particular number of inches. When these inches relate to a period of time, the measures corresponding to these numbers must relate to movement. Furthermore, measures derived from time cycles expressed in inches can also be indicative of a geometrical relationship expressed in metres.
At Giza, several measures in inches correspond to an astronomical cycle. For example, the east-west distance between the westernmost side of the third pyramid and the easternmost side of the Great Pyramid (i.e. the width of the rectangle encompassing these two pyramids) is, according to Flinders Petrie, 29 227.199 inches116. This can be interpreted as 29.53125 x 12 x 4 x 20.61883527 inches, or 29.53059 x 12 x 4 x 20.6192961 inches, which is 4 lunar years expressed in royal Egyptian cubits. It is also 80 x 365.3399875 inches, which is very close to 80 solar years.117 This offers a clue to a possible correspondence in ancient time reckoning between a period of 80 years and 4 lunar years, as 80 years in days, divided by 4 lunar years in days, give 20.61377705, a possible value for a cubit in inches. Converted to metres from inches, this value is very close to pi -Phi2 , which Schwaller de Lubicz demonstrated is one expression of an Egyptian royal cubit in metres. In fact, if a metre were to correspond to this relationship between the lunar and solar years together with the difference between pi and Phi2, it might be thought of, in inches, as:
80 x 365.242199 / 29.53059 x 4 x 12 x (π-((√5 + 3)/2))) = 39.372430315
(With 864/275 and 144/55 for pi and Phi2, the result would be 39.366588, and 39.366 inches is 54 digits of 0.729 inches)
Another example of the use of the inch expressing a unit of time can be found in the mean side of the Great pyramid (given by Flinders Petrie as 9068.8 inches) combined with the mean side of the third pyramid, given by him as 4153.6 inches. The product of these two measures is equivalent to 3,000 x 29.53059 square cubits, each measuring 20.62 inches. The significance of 3,000 lunations can perhaps be found in the relation between the solar and lunar years can be expressed as pi multiplied by the length of a precessional cycle, as 25920 years, divided by 30,000. So, with 22/7 for pi, and the number 10.875119 as the difference in days between twelve lunar months and a solar year, 3,000 x 10 x 29.53059 / 10.875119 x 7/22 = 25,919.992.


An example of the use of the metre expressing a lunar period of time, can also be found in the base of the Great Pyramid, if a 52 week calendar, which belongs as much to the cycles of the Maya and Aztecs as to the modern calendar, is applied. The pyramid base is 9068.8 inches per mean side, and 36 275.2 inches for the perimeter, which is 921.39008 metres. Divided by 52, this is 17.71904. Multiplied by 10, this is the number of days in 6 lunar months. Divided by 6, this figure gives a lunar month of 29.5317333, which is very close to the current estimate of 29.53059. It would be a perfect match if we reduced slightly the figure for the mean base side to 9068.448888 inches, which is well within Flinders Petrie's parameters, or if we worked with a ratio of 39.371603 inches per metre.118 If the perimeter of the Great Pyramid corresponds to 6/10 lunar months, in modern metres, then one side can be thought of as 29.53059 days, a lunation, multiplied by the number of 7 day weeks in a calendar year, 52, multiplied by 3/20, which equals 230.338602 metres, or 9068.448888 inches.
These examples demonstrate that units of measure were used in ancient Egypt, in this case, specifically at Giza, to express periods of time, often expressed in moon cycles, and that the inch and the metre were used for this purpose.119 Elsewhere in the ancient world, the units of measure were also used to express movement.
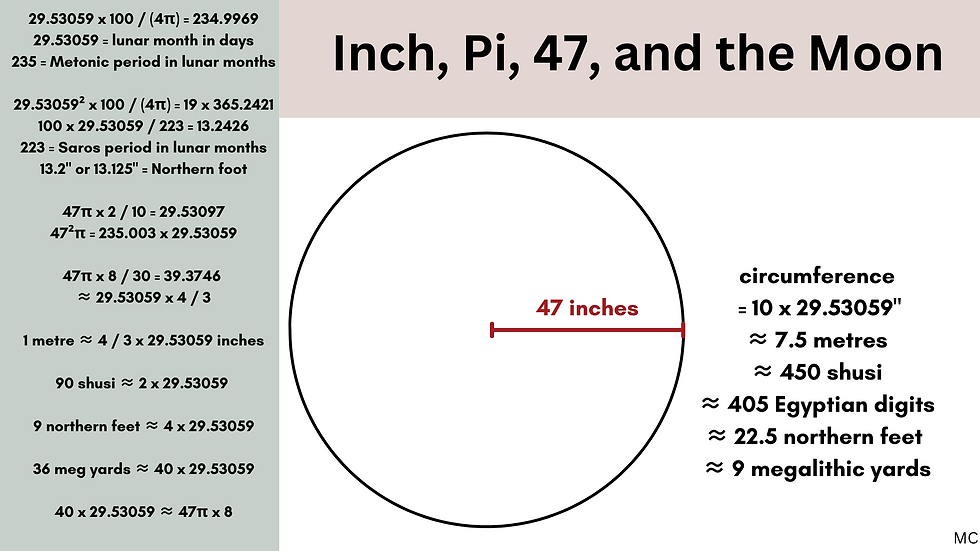
Jim Wakefield has demonstrated that at the Rollright stones in England, the lunar month could be expressed as 47π/5, which is 29.5309709, and the Metonic cycle of 19 years of 235 lunar months could be expressed as 472π. Incredibly, these two approximations can be found in one circle, with a radius of 47 units, the lunar month being expressed by the circumference, and the Metonic cycle being expressed by the area.120 The unit used at the Rollright Stones is the Northern or Saxon foot, of 13.2 inches, three of which make a Saxon wand of 39.6 inches. the Saxon wand relates to the 39.375 inch metre with the fraction 175/176, the same fraction which links two approximations of pi, 25/8 and 22/7. Jim Wakefield has observed that the great circle at Stanton Drew is exactly 36 times the circumference of the Rollrights, and features 36 standing stones. He also shows that at Stonehenge, the outer edge of the Sarsen circle can be interpreted as having a diameter of 94 Saxon feet, so that the circumference is then 295.3097 Saxon feet, or almost exactly 100 lunations. The Sarsen circle as measured from the centres of the stones can be interpreted as 90 Saxon feet, and this gives a circumference of just under 200 x √2 Saxon feet, with calculator pi, or exactly 99/70 x 200 Saxon feet with 22/7 or pi. The Northern or Saxon foot itself can be understood as 47 x 2 / 70 x π2 inches, and the metre as 47 x 4 / 15 x π inches. Pi can be understood as central to the measure of time through the moon’s cycles, as it can be approximated by a lunation of 29.53059 days multiplied by the difference in days between a solar and lunar year, 10.87512, multiplied by 1000/864. And, using 22/7 or pi and 99/70 for the square root of 2, you can obtain a 39.375 inch metre in the following way: 12 x 29.53125 x 22/7 x 70/99 x 1/20 = 39.375.
(Alternatively, using the calculator approximations for the irrationals, you could do: 12 x 29.53059 x pi / (20 x √2) = 39.3602363. )





The Sarsen circle diameter between the inner sides of the stones is according to Flinders Petrie 1167.9 inches, but taken as 1162.76699 inches, slightly over a 5 inch difference, this can be interpreted as 29.53059 metres of 39.375 inches, and the circumference is then 254 x 365.242 / 1000 metres of 39.375 inches. As we have already seen, 10 000 / 254 inches is the modern value of the metre in inches.
Richard Heath and Robin Heath’s work at Le Manio in Brittany, France, also demonstrates that units of measure could express movement, and also show the importance of the inch in megalithic structures, through the geometry of a rectangle.121 In particular, 4/3 inch encodes a measure of time in days, as 29.53125, taken as a value for a lunation expressed in units of 4/3 inches are 39.375 inches. They show that a rectangle made up of 4 squares has interesting solar and lunar properties. This rectangle is made up of two 1:4:√17 triangles. The width, as 9 metres, represents 12 lunar months, or a lunar year. The length is 36 metres, representing 48 lunar months, or 4 lunar years (like the Giza rectangle width, mentioned earlier). And the diagonal represents 4 solar years in inches. 4 lunar months as 29.53125 days make 118.125 days. 118.125 inches are 100 Egyptian feet, and also 3 metres of 39.375 inches.
The metre joins the megalithic yard as a measure naturally generated by day-inch counting, in this case useful for the reproduction of longer time periods without a day count or suitable longer rope. Metres can make lunar base lines and reproduce the four squares geometry whilst containing within them the original day-inch count for the lunar month.122

The metre makes sense as a value in inches, as part of the geometries of the circle and quadruple square, in the context of time measurement in ancient megalithic sites. This is ironic in view of the fact that the 20th century inch has been defined in terms of the metre, but either way, it underlines the importance of the connection between these two units. There are many ways in which a 39.375 inch metre can relate geometrically to the inch, or to a foot of 12 inches. Below are two examples.


Making connections between the metric and imperial systems with a 39.375 conversion ratio allows us to see that 20 mm of a 39.375 inch metre are a 7.875 inches, which, when multiplied by Phi squared, especially a nice approximation such as 144/55 or 55/21, give us the Egyptian royal cubit, which is also a metre multiplied by pi (again a nice approximation such as 22/7 or 864/275 works well) and then divided by 6. And 0.8 yards are being related to a Persian cubit of 28.8 inches or 5.12 / 7 mm, as Mauss claims. There is a lot that remains to be discovered about the origins of current measuring systems, such as imperial, and how it is geodesic when, officially, our planet was only successfully measured in recent centuries. We might also think of other units as values in inches, such as an Egyptian foot of 11.8125 inches as 29.53125/25 x 10 inches, or a shusi as 29.53125/90 x 2 =0.65625 inches, a digit as 29.53125 x 2/81 = 0.7291666667 inches, or a Roman foot as 1082/1 000 = 11.664 inches.

The Modern Metre
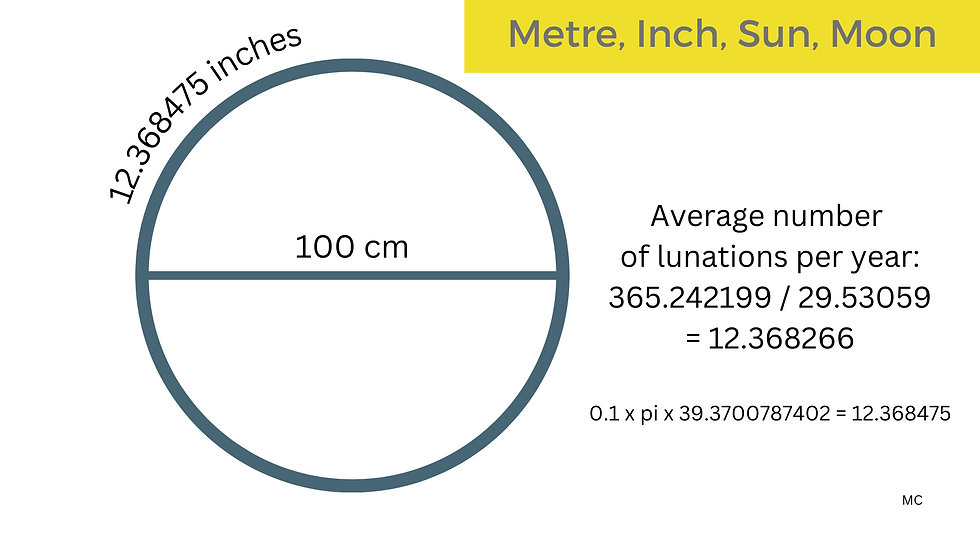
Even though the 10 000/254 inch metre (the current one) isn't quite as user friendly, in that respect, as the 39.375 inch metre, it does also offer some nice theoretical connections. For example, we could look for a meaningful comparison to the cycles of the moon and sun. 254 years are approximately 1,000 lunations. The relationship between these two cycles, 254 years and 1000 lunations, seems central to the inch / metre ratio.

Phi squared modern metres x 29.53059 x 12/10 = 365.2534037 inches. This suggests that Phi squared/100 metres corresponds approximately to the ratio between a solar and a lunar year. Also, 10 solar years in inches are approximately 1 lunation x pi metres.


Jim Wakefield has found very intriguing connections between imperial and metric in the dimensions of the glass pyramid at the Louvre. In a blog post123, he wrote:
Many people believe there is no relationship re metric and imperial measure. I certainly thought that until I found quite by accident two measures and this may be only a coincidence but worth recording.
The solar year and the lunar year. 365.25 days and lunar 354.3 days.
If you can imagine a solar year being a circle 365.25 days find the diameter = 116.2626 and call this feet.
116.2626 feet = 35.4368 metres.
And we know this is accurate as 35.4368 / 12 = 2.95306 and that is pretty good 29.53 days in a synodic month really 29.5306
With pleasure I wish to add a remarkable fact re the dimensions of this glass pyramid and to the cleverness of its architects. This may be common knowledge among architects but for me it was a discovery.
Length of base given in drawing 35.42 metres. I am not sure if these figures are absolutely correct so if anyone knows then let me knows please.
Height 21.64 metres.
I asked myself why the odd numbers? Why not just 35 metres? for the base and 21 for the height.
Then I looked at the number 35.42 and thought about the closeness of this number to that of a moon based year.
A synodic month = 29.53059 days x 12 months 354.36 days close to the number given 35.42. Ok that is easily shaken off as a coincidence but look.
As in the drawing the length given is 35.42 metres now remember Pei the architect is an American and as I have been informed was living in his Manhattan home in January 2016 he turns 100 on the 27th April this year 2017. I looked at this odd number and converted to feet 35.42m = 116.20734 feet and I saw it straight away.
A circle inscribed into the base of the pyramid at the Louvre measures 365.076 feet 365 the number of days in a year.
By switching from metric to Imperial the architect has given the lengths for a lunar and solar year. 354 and 365. Interesting that the metre allows this??
And not only that he has done it again in the height as he has doubled his base length 35.42 x 2 = 70.84 and named this number FEET.
70.84 FEET = 21.6m. Not sure exactly which value for pi he used but so clever.

Louvre Pyramid, my photo
Twelve synodic months of 29.53059 days make a lunar year of 354.36708 days.
Convert a value of 35.436708 metres to imperial feet, so multiply by 10,000/(254 x 12), the result is 116.26216535 feet. Multiply by pi, top convert this measure, as the diameter of a circle, to obtain the circumference, the result is 365.24836 feet.

Jim Wakefield has found something very curious about the relation between metric and imperial, which could well go some way to explain why, after scientists busied themselves for so long with microscopes measuring the inch in relation to the metre and vice versa, with various standards at various temperatures, in the end a seemingly random 10,000/254 rate was chosen. Take 365.242199 feet as the circumference of a circle, then divide by pi to find the diameter, convert to modern metres, you will get 35.4361098 m. There are 365.242199 days in an average solar year and 354.36708 days in an average lunar year (of 12 synodic months). In other words a circle representing ten years in imperial feet will have a diameter of one lunar year in metres. The 10,000/254 ratio works here perfectly because a circle representing 254 years will have a dimension of 1,000 lunar months. (29.53059 x 1,000 x pi / 365.242199 = 254.0042877) This is found at Stonehenge, as seen above, where the Sarsen circle diameter between the inner sides of the stones, given as 1167.9 ±0.7 inches by Flinders Petrie, but which perhaps can be taken as 1162.8 inches to make 29.53059 metres of 39.375 inches (or 29.53059 x 39.5488 inches). The circumference then becomes 254 x 365.242 / 1000 metres, which is equal to 3652.42 inches. The inner blue stone circle diameter is given by Petrie as 472.2 inches, which can be interpreted as 12 x 39.375 inches, can also be taken as a measure of time, as the number of months in a year. The Sarsen diameter divided by 29.53059 and multiplied by 12 gives the Bluestone diameter, to within 2.4 inches, as per Flinders Petrie’s measures.
The calculator value for pi is slightly different to the value produced by the following calculation:
365.242199 / 35.436708 x 12 / 39.3700787402 = 3.141539622. A value for the metre of 39.36941454 inches would work well with calculator pi. There is also a possible Phi squared relation: twelve lunar months of 29.53059 days x 2.618033 divided by a solar year in days, 365.242199, and by 1100, gives 39.3688258. This could be equated to a slightly shorter metre in inches.
The imperial foot (which John Neal has identified as “one of the variations of what are accepted as Greek measure, variously called Olympian or Geographic”124) becomes associated with the sun, and the metre with the moon.
Another interesting metre / inch / moon connection involves the number 153, of the biblical fish story, and the number 47. Researchers Jim Wakefield and Dennis Payne have both found the number 47 has interesting lunar connections, because 47 x 2 x pi/10 = 29.53097, which is very close to a lunar month in days, and 47² x pi = 6,939.77817, which is very close to the number of days in a Metonic cycle of 19 years. 153/(28 x 47) inches are 29.530395 modern metres. You could interpret the Aubrey circle as 29.53059 metres (inner diameter), and the mean side of the Great Pyramid of Giza as 29.53059 metres x 78/10.
Pi x47² is also approximately 153 x 254 x 10 / (28 x 2), which means the Metonic cycle can be written as 1530/56 inches converted to metres. Or 1 metre can be written as approx 153 x 10 000 / (28 x 47 x 29.53059) = 39.3698189 inches.
At any rate, the connections provided are a reminder that we don't always need to be looking for whole numbers of units in when we try and make sense of structures through their dimensions, as Petrie claims in his introduction to Inductive Metrology. If Jim Wakefield's analysis is right, then we can't underestimate the importance of the astronomical cycles in analysing measures that have been used in designs in prominent, or highly symbolic places. We might also ask ourselves why, historically, astronomers have taken an interest in metrology. It is possible that the metre has long associations with the moon, which have been carried on to this day.
Concluding remarks
For the past few centuries, there have been many ratios put forward by the eminent scientists and historians of the day to describe the precise relationship between the English and French units of measure. It was not until the 20th century that a single value was finally produced and adhered to.
This study is the result of confusion about the historical values for the metre given in inches, and why they were so varied until the 20th century. The lunar and solar connections between the inch and metre, and the analysis of various megalithic sites using the metre are intriguing. Perhaps the metre is just as an ancient as the inch. While the UK is no longer required to “trade in metric units”, we can remind ourselves that the imperial units have been calibrated in terms of the metre, so that 254 centimetres are 100 inches exactly. Fans of imperial might find solace in the hypothesis that the metre, as found in megalithic sites, may have existed as a particular number of inches, corresponding to a lunar cycle.
Discussions around Brexit have brought to the fore the history and importance of the units of measure used in the United Kingdom. Studying them can speak volumes (no pun intended) about the history of Britain and its links to Europe and the Middle East. The mysterious relationship between the inch and the metre is at any rate not just a thing of the distant past, as Jim Wakefield has demonstrated with his analysis of the Louvre pyramid.
Laplace’s involvement in the design of the metre is also intriguing. When Méchain and Delambre were busy measuring the meridian between Dunkerque and Barcelona, to determine the length of the new metre, they were closely supervised by Laplace. This is clear from reading Delambre's account: Laplace seems to have acted as a head scientist (his name is mentioned by Delambre in relation to refraction, the determination of the latitude of the Pantheon in Paris, and tables) but also as a supervisor. 17 The small errors which Méchain and Delambre made in their work are not relevant to the metre, as it exists now and as it existed from the start, as the provisional metre. Despite all the scientific effort, not to mention the hardship that Méchain and Delambre went through in their journey from Dunkirk to Barcelona, in the end the ratio between the new metre and the imperial yard was fixed over a century later, as an easy fraction, reflecting a curious quirk of sun and moon’s cycles. In the end, perhaps Laplace was looking for Méchain and Delambre to find something he already knew, that fitted in a system he wanted to use as a basis.
Perhaps the metric and imperial systems are designed to co-exist, in a dual system that mimics the eyes of Horus, that is, the sun and the moon. At any rate, they will probably coexist on packaging exported from the UK for some time, as the imperial values are revived. An “ancient liberty”, as Boris Johnson described the imperial system, may well in fact characterise the use of both the metre and the inch, as well as a whole array of ancient measures, all interlinked by astronomy and geometry.
Bibliography
Berriman, Algernon Edward, 1953, Historical Metrology: A New Analysis of the Archaeological and the Historical Evidence Relating to Weights and Measures, Dent
Badshah, Nadeem, “Boris Johnson to reportedly bring back imperial measurements to mark platinum jubilee”, The Guardian, Sat 28 May 2022, Boris Johnson to reportedly bring back imperial measurements to mark platinum jubilee | Brexit | The Guardianhts reserved. (modern)
Cagnazzi, Luca de Samuele, 1808, Elementi dell'arte statistica, Parte prima, Napoli Nella Stamperia Flautina
Flinders Petrie, W.M., 1893, The Pyramids and Temples of Gizeh, The Pyramids and Temples of Gizeh: Table of Contents (ronaldbirdsall.com)
Flinders Petrie, W.M. 1877, Inductive Metrology; or, the recovery of ancient measures from the monuments, Hargrove Saunders
Flinders Petrie, M.W. 1911, "Weights and Measures", Encyclopædia Britannica 1911 Encyclopædia Britannica/Weights and Measures - Wikisource, the free online library
Franklin, Hugh, 2000, “Earth, Pi, Miles and the Barleycorn”, http://hew_frank.tripod.com/epmb2.htm
Gosselin, Pascal F. J. 1790, Géographie des Grecs analysée: ou, Les systêmes d'Eratosthenes, de Strabon et de Ptolémée comparés entre eux et avec nos connoissances modernes, Imprimerie de Didot l’Ainé, Paris
Guilhiermoz, Paul, De l'équivalence des anciennes mesures. A propos d'une publication récente, Bibliothèque de l'École des chartes Année 1913 74 pp. 267-328, De l'équivalence des anciennes mesures. A propos d'une publication récente - Persée (persee.fr)
Heath, Robin, and Michell, John, 2005, The Lost Science of Measuring the Earth, Adventures Unlimited Press
Hussey, Robert, 1836, An Essay on the Ancient Weights and Money, and the Roman and Greek liquid measures, with an appendix on the Roman and Greek foot, S. Collingwood, Oxford. An essay on the ancient weights and money, and the Roman and Greek liquid measures, with an appendix on the Roman and Greek foot : Hussey, Robert, 1801-1856 : Free Download, Borrow, and Streaming : Internet Archive
Kelly, P. 1816, Metrology, or, an Exposition of Weights and Measures, Parliamentary Reports, London
Larzillière, E-F, 1839, Le Manuel des Poids et Mesures des Pas-de-Calais
Letronne, Jean-Antoine, 1851, Recherches Critiques, Historiques et Géographiques sur les fragments d’Héron d’Alexandrie. Imprimerie Nationale, Paris
Mauss, C. 1892, "L’Eglise de Saint Jérémie a Abou Gosch, Observations sur plusieurs mesures de l’antiquité (Suite)", in Revue Archéologique Troisième Série, T. 20 (Juillet-décembre 1892), pp. 232-253 (22 pages) Published by: Presses Universitaires de France
Méchain, Pierre & Delambre, Jean-Baptiste, 1810, Base du système métrique décimal, ou mesure de l'arc du méridien compris entre les parallèles de Dunkerque et Barcelone: executée en 1792 et années suivantes : suite des Mémoires de l'Institut, Volume 3, Baudouin
Neal, John, 2017, Ancient Metrology, Vol II: the Geographic Correlation, The Squeeze Press, Glastonbury
Neal, John, 2003, “ AOM: Ancient Measurement Systems: Their fractional integration,”, Graham Hancock.com
Nelson, Robert A, 1981, “Foundations of the international system of units (SI)”, Nelson-FoundationsSI.pdf (umd.edu)
Olinthus, Gregory, 1836, Mathematics for practical men: being a common-place book of principles, theorems, rules, and tables, in various departments of pure and mixed mathematics, with their application; especially to the pursuits of surveyors, architects, mechanics, and civil engineers, Philadelphia, E. L. Carey and A. Hart
Prony, R., Des expériences faites avec un instrument français et un instrument anglais, pour déterminer le rapport du mètre au pied anglais, et pour comparer entre eux les étalons originaux de mesure appartenant à l'Institut national de France, Lus à la séance publique de l'Institut national du 15 nivose an 10. In Base du système métrique décimal, ou mesure de l'arc du méridien ..., Volume 3: executée en 1792 et années suivantes : suite des Mémoires de l'Institut
Sears, J. E., et al. “A New Determination of the Ratio of the Imperial Standard Yard to the International Prototype Metre.” Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, vol. 227, 1928, pp. 281–315. JSTOR, http://www.jstor.org/stable/91218. Accessed 24 Jun. 2022.
Talleyrand Périgord Charles Maurice de. Discours non prononcé de M. de Talleyrand, évêque d'Autun, sur les poids et mesures, en annexe de la séance du 9 mars 1790. In: Archives Parlementaires de 1787 à 1860 - Première série (1787-1799) Tome XII - Du 2 mars au 14 avril 1790. Paris : Librairie Administrative P. Dupont, 1881. pp. 104-108.
Wakefield, Jim, From the Rollrights to Stonehenge, (2) From the Rollrights to Stonehenge | jim wakefield - Academia.edu
Wilkins, John, 1668, An Essay Towards a Real Character, and A Philosophical Language. WilkinsTranslationLong (metricationmatters.com)




I think that the ancients smoothed 29.53064125 to be 29.333... as follows
29.53064125 x 223/224.5 = 29.333... exactly
This puts 449 x 14.666... in the saros of exactly 6585.333... per the NASA website
18 years 11 days and 8 hours.
14.666... x 360 is then 5280
An astronomical source of the mile? I know you have alluded to this.
When the distance from Old sarum to Avebury is 23.333 miles the circumference of Avebury round Old Sarum is 146.666 miles.
This is a brilliant article Melissa. I have attached it to my latest meg yard post on academia.
https://www.academia.edu/s/5c13650fb2#comment_1150447
you mention 45 digits in the meg yard and consequently there must be 50000/1760 in the geodetic cubit.
Dave